4. 下列各种现象属于中心投影的是(
A. 晚上人走在路灯下的影子
B. 中午用来乘凉的树影
C. 上午人走在路上的影子
D. 早上升旗时地面上旗杆的影子
A
)A. 晚上人走在路灯下的影子
B. 中午用来乘凉的树影
C. 上午人走在路上的影子
D. 早上升旗时地面上旗杆的影子
答案:
A
5. 下面的四幅图中,灯光与影子的位置最合理的是(
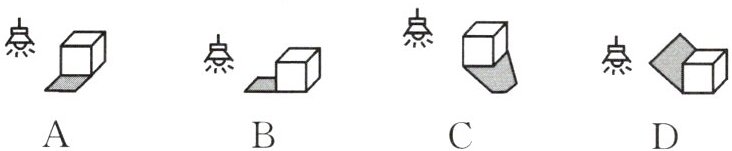
C
)
答案:
C
6. 下列是描述小明和小颖在同一盏路灯下影子的图片,其中合理的是(
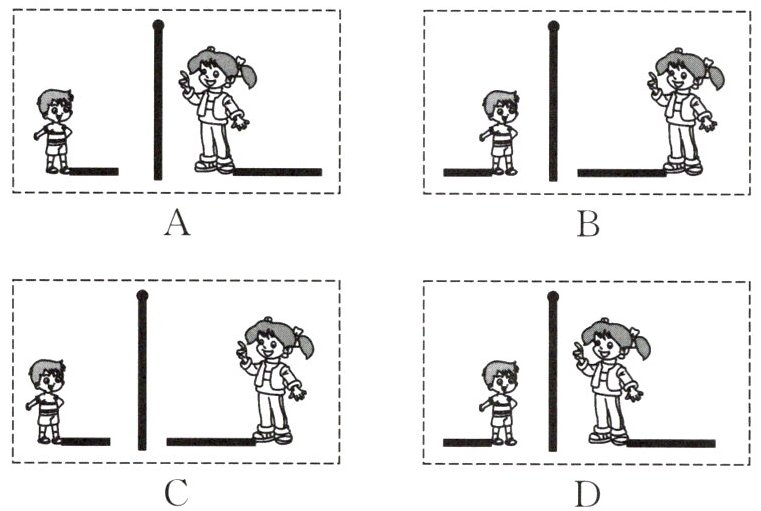
D
)
答案:
D
7. 如图,晚上小明在路灯下沿路从A处径直走到B处,这一过程中他在地上的影子(

A. 一直都在变短
B. 先变短后变长
C. 一直都在变长
D. 先变长后变短
B
)
A. 一直都在变短
B. 先变短后变长
C. 一直都在变长
D. 先变长后变短
答案:
B
8. 如图,有三根等高的标杆整齐划一地排列在马路的一侧,AB,CD,EF分别代表这三根标杆,MB为标杆AB在路灯下的影子,ND为标杆CD在路灯下的影子。
(1)画出路灯O的位置;
(2)画出标杆EF在路灯下的影子FH。

(1)画出路灯O的位置;
(2)画出标杆EF在路灯下的影子FH。

答案:
解:
(1)如图,点O为所作;
(2)如图,FH为所作。

解:
(1)如图,点O为所作;
(2)如图,FH为所作。

9. 如图,在平面直角坐标系中,点$P(3,2)$是一个光源,木杆AB两端的坐标分别为$A(0,1),B(4,1)$。则木杆AB在x轴上的投影长为(
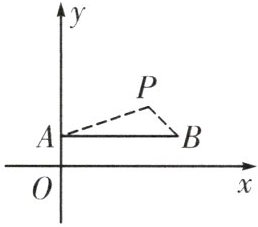
A. 4
B. 5
C. 6
D. 8
D
)
A. 4
B. 5
C. 6
D. 8
答案:
D
10. 如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,$AB// CD,AB=1.5m,CD=4.5m$,点P到CD的距离为2.7 m,求AB与CD间的距离。
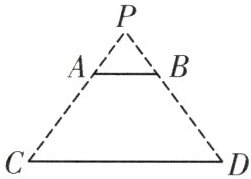
解:∵AB//CD,
∴△PAB∽△PCD。
假设CD到AB的距离为x m,则$\frac{AB}{CD}=\frac{2.7−x}{2.7}$,$\frac{1.5}{4.5}=\frac{2.7−x}{2.7}$,x=
答:AB与CD间的距离是

解:∵AB//CD,
∴△PAB∽△PCD。
假设CD到AB的距离为x m,则$\frac{AB}{CD}=\frac{2.7−x}{2.7}$,$\frac{1.5}{4.5}=\frac{2.7−x}{2.7}$,x=
1.8
。答:AB与CD间的距离是
1.8
m。
答案:
解:
∵AB//CD,
∴△PAB∽△PCD。
假设CD到AB的距离为x m,则$\frac{AB}{CD}=\frac{2.7−x}{2.7}$,$\frac{1.5}{4.5}=\frac{2.7−x}{2.7}$,x=1.8。
答:AB与CD间的距离是1.8m。
∵AB//CD,
∴△PAB∽△PCD。
假设CD到AB的距离为x m,则$\frac{AB}{CD}=\frac{2.7−x}{2.7}$,$\frac{1.5}{4.5}=\frac{2.7−x}{2.7}$,x=1.8。
答:AB与CD间的距离是1.8m。
11. 如图,身高1.6 m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部A处向东走20步到M处,发现自己的影子端点刚好在点P处,继续向东走5步到P处,此时影子的端点在Q处。
(1)根据题意画图,找出路灯O的位置。
(2)求路灯的高和影长PQ。

(1)根据题意画图,找出路灯O的位置。
(2)求路灯的高和影长PQ。

答案:
解:
(1)如图,点O为路灯的位置;
(2)作OA垂直地面,如图,AM=20步,MP=5步,MN=PB=1.6m,
∵MN//OA,
∴△PMN∽△PAO,
∴$\frac{MN}{OA}=\frac{PM}{PA}$,即$\frac{1.6}{OA}=\frac{5}{5+20}$,解得OA=8(m),
∵PB//OA,
∴△QPB∽△QAO,
∴$\frac{PB}{OA}=\frac{PQ}{QA}$,即$\frac{1.6}{8}=\frac{PQ}{PQ+25}$,解得PQ=$\frac{25}{4}$(步)。

解:
(1)如图,点O为路灯的位置;
(2)作OA垂直地面,如图,AM=20步,MP=5步,MN=PB=1.6m,
∵MN//OA,
∴△PMN∽△PAO,
∴$\frac{MN}{OA}=\frac{PM}{PA}$,即$\frac{1.6}{OA}=\frac{5}{5+20}$,解得OA=8(m),
∵PB//OA,
∴△QPB∽△QAO,
∴$\frac{PB}{OA}=\frac{PQ}{QA}$,即$\frac{1.6}{8}=\frac{PQ}{PQ+25}$,解得PQ=$\frac{25}{4}$(步)。

查看更多完整答案,请扫码查看


