《2025年春如金卷课时作业AB本九年级数学上册北师大版》

A.黄金比是（B）

A. $\frac { \sqrt { 5 } + 1 } { 2 }$
B. $\frac { \sqrt { 5 } - 1 } { 2 }$
C. $\frac { \sqrt { 5 } \pm 1 } { 2 }$
D. 0.618

答案： B

B.如图，点C是AB的黄金分割点（AC＞BC），AB=4，则AC=$2 \sqrt { 5 } - 2$。

答案： 答案：$2 \sqrt { 5 } - 2$
解析：根据C为AB的黄金分割点，AC＞BC，得$\frac { A C } { A B } = \frac { \sqrt { 5 } - 1 } { 2 }$。
∵AB=4，
∴$A C = 4 × \frac { \sqrt { 5 } - 1 } { 2 } = 2 \sqrt { 5 } - 2$。

C.如图，在五角星图形中，AD=BC，C，D两点都是AB的黄金分割点，AB=1，求CD的长。

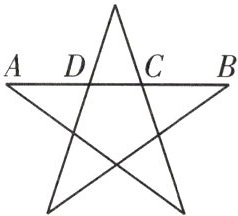
解：∵C，D两点都是AB的黄金分割点，
AC=BD=$\frac { \sqrt { 5 } - 1 } { 2 } A B = \frac { \sqrt { 5 } - 1 } { 2 }$，
∴$A D = A C - C D = \frac { \sqrt { 5 } - 1 } { 2 } - C D$，
∵AD=BC，
∴$B C = \frac { \sqrt { 5 } - 1 } { 2 } - C D$，
而AC+BC=AB，
∴$\frac { \sqrt { 5 } - 1 } { 2 } + \frac { \sqrt { 5 } - 1 } { 2 } - C D = 1$，
∴$C D = \sqrt { 5 } - 2$。

答案： $\frac { \sqrt { 5 } - 1 } { 2 } A B = \frac { \sqrt { 5 } - 1 } { 2 }$，$\frac { \sqrt { 5 } - 1 } { 2 } + \frac { \sqrt { 5 } - 1 } { 2 } - C D = 1$

1.把1m的线段进行黄金分割，则分成的较短的线段长为（A）
A. $\frac { 3 - \sqrt { 5 } } { 2 } m$
B. $\frac { \sqrt { 5 } - 1 } { 2 } m$
C. $\frac { \sqrt { 5 } + 1 } { 2 } m$
D. $\frac { 3 + \sqrt { 5 } } { 2 } m$

答案： A

2.如图，已知点C，D是线段AB的两个黄金分割点，若线段AB的长为10cm，求线段CD的长度。

解：∵点C，D是线段AB的两个黄金分割点，
∴AD=BC=$\frac{\sqrt{5}-1}{2}AB=\frac{\sqrt{5}-1}{2}×10=$5√5 - 5，
∴CD=AD+BC-AB=10√5 - 10-10=(10√5 - 20)cm。

答案： 解：
∵点C，D是线段AB的两个黄金分割点，
∴AD=BC=$\frac{\sqrt{5}-1}{2}AB=\frac{\sqrt{5}-1}{2}\times10=5\sqrt{5}-5$，
∴CD=AD+BC-AB=$10\sqrt{5}-10-10=(10\sqrt{5}-20)$cm。

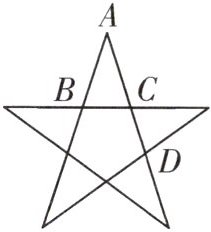
3.如图，正五角星中包含了许多黄金三角形，许多线段之间构成了黄金比，如点C是线段AD的黄金分割点（AC＞CD）。已知$B C = ( \sqrt { 5 } - 1 ) c m$，那么AC=2cm。

答案： 2