4. 用配方法解一元二次方程$-3x^{2}+12x-2=0$时,将它化为$(x+a)^{2}=b$的形式,则$a+b$的值为(
A. $\frac {14}{3}$
B. $\frac {10}{3}$
C. $\frac {16}{3}$
D. $\frac {4}{3}$
D
)A. $\frac {14}{3}$
B. $\frac {10}{3}$
C. $\frac {16}{3}$
D. $\frac {4}{3}$
答案:
D
5. 解下列方程:
(1)$(x-3)^{2}-4=0$;
(2)$x^{2}-4x-8=0$;
(3)$x^{2}-\frac {2}{3}x+\frac {1}{18}=0$;
(4)$x^{2}-2\sqrt {3}x+3=0$;
(5)$2x^{2}-7x+6=0$。
(1)$(x-3)^{2}-4=0$;
$x_{1}=5,x_{2}=1$
(2)$x^{2}-4x-8=0$;
$x_{1}=2+2\sqrt{3},x_{2}=2-2\sqrt{3}$
(3)$x^{2}-\frac {2}{3}x+\frac {1}{18}=0$;
$x_{1}=\frac{2+\sqrt{2}}{6},x_{2}=\frac{2-\sqrt{2}}{6}$
(4)$x^{2}-2\sqrt {3}x+3=0$;
$x_{1}=x_{2}=\sqrt{3}$
(5)$2x^{2}-7x+6=0$。
$x_{1}=2,x_{2}=\frac{3}{2}$
答案:
$(1)$ 解方程$(x - 3)^2 - 4 = 0$
解:
$\begin{aligned}(x - 3)^2 - 4 &= 0\\(x - 3)^2 &= 4\\x - 3 &= \pm\sqrt{4}\\x - 3 &= \pm2\end{aligned}$
当$x - 3 = 2$时,$x = 2 + 3 = 5$;
当$x - 3 = -2$时,$x = -2 + 3 = 1$。
所以$x_1 = 5$,$x_2 = 1$。
$(2)$ 解方程$x^2 - 4x - 8 = 0$
解:
对于一元二次方程$ax^2 + bx + c = 0$($a\neq0$),其求根公式为$x=\frac{-b\pm\sqrt{b^2 - 4ac}}{2a}$。
在方程$x^2 - 4x - 8 = 0$中,$a = 1$,$b = -4$,$c = -8$。
$\begin{aligned}\Delta &= b^2 - 4ac\\&= (-4)^2 - 4×1×(-8)\\&= 16 + 32\\&= 48\end{aligned}$
$\begin{aligned}x&=\frac{-(-4)\pm\sqrt{48}}{2×1}\\&=\frac{4\pm4\sqrt{3}}{2}\\&= 2\pm2\sqrt{3}\end{aligned}$
所以$x_1 = 2 + 2\sqrt{3}$,$x_2 = 2 - 2\sqrt{3}$。
$(3)$ 解方程$x^2 - \frac{2}{3}x + \frac{1}{18} = 0$
解:
方程两边同时乘以$18$得:$18x^2 - 12x + 1 = 0$。
对于一元二次方程$ax^2 + bx + c = 0$($a\neq0$),其求根公式为$x=\frac{-b\pm\sqrt{b^2 - 4ac}}{2a}$。
在方程$18x^2 - 12x + 1 = 0$中,$a = 18$,$b = -12$,$c = 1$。
$\begin{aligned}\Delta &= b^2 - 4ac\\&= (-12)^2 - 4×18×1\\&= 144 - 72\\&= 72\end{aligned}$
$\begin{aligned}x&=\frac{-(-12)\pm\sqrt{72}}{2×18}\\&=\frac{12\pm6\sqrt{2}}{36}\\&=\frac{2\pm\sqrt{2}}{6}\end{aligned}$
所以$x_1 = \frac{2 + \sqrt{2}}{6}$,$x_2 = \frac{2 - \sqrt{2}}{6}$。
$(4)$ 解方程$x^2 - 2\sqrt{3}x + 3 = 0$
解:
$\begin{aligned}x^2 - 2\sqrt{3}x + 3 &= 0\\(x - \sqrt{3})^2 &= 0\end{aligned}$
所以$x_1 = x_2 = \sqrt{3}$。
$(5)$ 解方程$2x^2 - 7x + 6 = 0$
解:
对于一元二次方程$ax^2 + bx + c = 0$($a\neq0$),其求根公式为$x=\frac{-b\pm\sqrt{b^2 - 4ac}}{2a}$。
在方程$2x^2 - 7x + 6 = 0$中,$a = 2$,$b = -7$,$c = 6$。
$\begin{aligned}\Delta &= b^2 - 4ac\\&= (-7)^2 - 4×2×6\\&= 49 - 48\\&= 1\end{aligned}$
$\begin{aligned}x&=\frac{-(-7)\pm\sqrt{1}}{2×2}\\&=\frac{7\pm1}{4}\end{aligned}$
当$x=\frac{7 + 1}{4}$时,$x = 2$;
当$x=\frac{7 - 1}{4}$时,$x = \frac{3}{2}$。
所以$x_1 = 2$,$x_2 = \frac{3}{2}$。
解:
$\begin{aligned}(x - 3)^2 - 4 &= 0\\(x - 3)^2 &= 4\\x - 3 &= \pm\sqrt{4}\\x - 3 &= \pm2\end{aligned}$
当$x - 3 = 2$时,$x = 2 + 3 = 5$;
当$x - 3 = -2$时,$x = -2 + 3 = 1$。
所以$x_1 = 5$,$x_2 = 1$。
$(2)$ 解方程$x^2 - 4x - 8 = 0$
解:
对于一元二次方程$ax^2 + bx + c = 0$($a\neq0$),其求根公式为$x=\frac{-b\pm\sqrt{b^2 - 4ac}}{2a}$。
在方程$x^2 - 4x - 8 = 0$中,$a = 1$,$b = -4$,$c = -8$。
$\begin{aligned}\Delta &= b^2 - 4ac\\&= (-4)^2 - 4×1×(-8)\\&= 16 + 32\\&= 48\end{aligned}$
$\begin{aligned}x&=\frac{-(-4)\pm\sqrt{48}}{2×1}\\&=\frac{4\pm4\sqrt{3}}{2}\\&= 2\pm2\sqrt{3}\end{aligned}$
所以$x_1 = 2 + 2\sqrt{3}$,$x_2 = 2 - 2\sqrt{3}$。
$(3)$ 解方程$x^2 - \frac{2}{3}x + \frac{1}{18} = 0$
解:
方程两边同时乘以$18$得:$18x^2 - 12x + 1 = 0$。
对于一元二次方程$ax^2 + bx + c = 0$($a\neq0$),其求根公式为$x=\frac{-b\pm\sqrt{b^2 - 4ac}}{2a}$。
在方程$18x^2 - 12x + 1 = 0$中,$a = 18$,$b = -12$,$c = 1$。
$\begin{aligned}\Delta &= b^2 - 4ac\\&= (-12)^2 - 4×18×1\\&= 144 - 72\\&= 72\end{aligned}$
$\begin{aligned}x&=\frac{-(-12)\pm\sqrt{72}}{2×18}\\&=\frac{12\pm6\sqrt{2}}{36}\\&=\frac{2\pm\sqrt{2}}{6}\end{aligned}$
所以$x_1 = \frac{2 + \sqrt{2}}{6}$,$x_2 = \frac{2 - \sqrt{2}}{6}$。
$(4)$ 解方程$x^2 - 2\sqrt{3}x + 3 = 0$
解:
$\begin{aligned}x^2 - 2\sqrt{3}x + 3 &= 0\\(x - \sqrt{3})^2 &= 0\end{aligned}$
所以$x_1 = x_2 = \sqrt{3}$。
$(5)$ 解方程$2x^2 - 7x + 6 = 0$
解:
对于一元二次方程$ax^2 + bx + c = 0$($a\neq0$),其求根公式为$x=\frac{-b\pm\sqrt{b^2 - 4ac}}{2a}$。
在方程$2x^2 - 7x + 6 = 0$中,$a = 2$,$b = -7$,$c = 6$。
$\begin{aligned}\Delta &= b^2 - 4ac\\&= (-7)^2 - 4×2×6\\&= 49 - 48\\&= 1\end{aligned}$
$\begin{aligned}x&=\frac{-(-7)\pm\sqrt{1}}{2×2}\\&=\frac{7\pm1}{4}\end{aligned}$
当$x=\frac{7 + 1}{4}$时,$x = 2$;
当$x=\frac{7 - 1}{4}$时,$x = \frac{3}{2}$。
所以$x_1 = 2$,$x_2 = \frac{3}{2}$。
6. 用配方法解方程$3x^{2}-6x+2=0$,将方程变为$(x-m)^{2}=\frac {1}{3}$的形式,则$m$的值为(
A. 9
B. -9
C. 1
D. -1
C
)A. 9
B. -9
C. 1
D. -1
答案:
C
7. 解下列方程:
(1)$3x^{2}+6\sqrt {2}x-1=0$;
(2)$6x^{2}-x-3=0$;
(3)$2x^{2}-\sqrt {2}x-30=0$;
(4)$\frac {1}{4}x^{2}-6x+3=0$。
(1)$3x^{2}+6\sqrt {2}x-1=0$;
$x_{1}=\frac{-3\sqrt{2}+\sqrt{21}}{3},x_{2}=\frac{-3\sqrt{2}-\sqrt{21}}{3}$
(2)$6x^{2}-x-3=0$;
$x_{1}=\frac{1+\sqrt{73}}{12},x_{2}=\frac{1-\sqrt{73}}{12}$
(3)$2x^{2}-\sqrt {2}x-30=0$;
$x_{1}=3\sqrt{2},x_{2}=-\frac{5}{2}\sqrt{2}$
(4)$\frac {1}{4}x^{2}-6x+3=0$。
$x_{1}=12+2\sqrt{33},x_{2}=12-2\sqrt{33}$
答案:
$(1)$ 解方程$3x^{2}+6\sqrt {2}x - 1 = 0$
解:对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$,其求根公式为$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$。
在方程$3x^{2}+6\sqrt {2}x - 1 = 0$中,$a = 3$,$b = 6\sqrt{2}$,$c=-1$。
先计算判别式$\Delta=b^{2}-4ac=(6\sqrt{2})^{2}-4×3×(-1)=72 + 12=84$。
将$a$、$b$、$\Delta$代入求根公式可得:
$x=\frac{-6\sqrt{2}\pm\sqrt{84}}{2×3}=\frac{-6\sqrt{2}\pm2\sqrt{21}}{6}=\frac{-3\sqrt{2}\pm\sqrt{21}}{3}$
即$x_1=\frac{-3\sqrt{2}+\sqrt{21}}{3}$,$x_2=\frac{-3\sqrt{2}-\sqrt{21}}{3}$。
$(2)$ 解方程$6x^{2}-x - 3 = 0$
解:在方程$6x^{2}-x - 3 = 0$中,$a = 6$,$b=-1$,$c = -3$。
计算判别式$\Delta=b^{2}-4ac=(-1)^{2}-4×6×(-3)=1 + 72 = 73$。
代入求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$得:
$x=\frac{1\pm\sqrt{73}}{2×6}=\frac{1\pm\sqrt{73}}{12}$
即$x_1=\frac{1+\sqrt{73}}{12}$,$x_2=\frac{1-\sqrt{73}}{12}$。
$(3)$ 解方程$2x^{2}-\sqrt {2}x - 30 = 0$
解:在方程$2x^{2}-\sqrt {2}x - 30 = 0$中,$a = 2$,$b=-\sqrt{2}$,$c = -30$。
计算判别式$\Delta=b^{2}-4ac=(-\sqrt{2})^{2}-4×2×(-30)=2 + 240 = 242$。
代入求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$得:
$x=\frac{\sqrt{2}\pm\sqrt{242}}{2×2}=\frac{\sqrt{2}\pm11\sqrt{2}}{4}$
即$x_1=\frac{\sqrt{2}+11\sqrt{2}}{4}=3\sqrt{2}$,$x_2=\frac{\sqrt{2}-11\sqrt{2}}{4}=-\frac{5\sqrt{2}}{2}$。
$(4)$ 解方程$\frac{1}{4}x^{2}-6x + 3 = 0$
解:方程两边同时乘以$4$化为一般形式$x^{2}-24x + 12 = 0$,此时$a = 1$,$b=-24$,$c = 12$。
计算判别式$\Delta=b^{2}-4ac=(-24)^{2}-4×1×12=576 - 48 = 528$。
代入求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$得:
$x=\frac{24\pm\sqrt{528}}{2}=\frac{24\pm4\sqrt{33}}{2}=12\pm2\sqrt{33}$
即$x_1=12 + 2\sqrt{33}$,$x_2=12 - 2\sqrt{33}$。
综上,$(1)$ $x_1=\frac{-3\sqrt{2}+\sqrt{21}}{3}$,$x_2=\frac{-3\sqrt{2}-\sqrt{21}}{3}$;$(2)$ $x_1=\frac{1+\sqrt{73}}{12}$,$x_2=\frac{1-\sqrt{73}}{12}$;$(3)$ $x_1=3\sqrt{2}$,$x_2=-\frac{5\sqrt{2}}{2}$;$(4)$ $x_1=12 + 2\sqrt{33}$,$x_2=12 - 2\sqrt{33}$。
解:对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$,其求根公式为$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$。
在方程$3x^{2}+6\sqrt {2}x - 1 = 0$中,$a = 3$,$b = 6\sqrt{2}$,$c=-1$。
先计算判别式$\Delta=b^{2}-4ac=(6\sqrt{2})^{2}-4×3×(-1)=72 + 12=84$。
将$a$、$b$、$\Delta$代入求根公式可得:
$x=\frac{-6\sqrt{2}\pm\sqrt{84}}{2×3}=\frac{-6\sqrt{2}\pm2\sqrt{21}}{6}=\frac{-3\sqrt{2}\pm\sqrt{21}}{3}$
即$x_1=\frac{-3\sqrt{2}+\sqrt{21}}{3}$,$x_2=\frac{-3\sqrt{2}-\sqrt{21}}{3}$。
$(2)$ 解方程$6x^{2}-x - 3 = 0$
解:在方程$6x^{2}-x - 3 = 0$中,$a = 6$,$b=-1$,$c = -3$。
计算判别式$\Delta=b^{2}-4ac=(-1)^{2}-4×6×(-3)=1 + 72 = 73$。
代入求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$得:
$x=\frac{1\pm\sqrt{73}}{2×6}=\frac{1\pm\sqrt{73}}{12}$
即$x_1=\frac{1+\sqrt{73}}{12}$,$x_2=\frac{1-\sqrt{73}}{12}$。
$(3)$ 解方程$2x^{2}-\sqrt {2}x - 30 = 0$
解:在方程$2x^{2}-\sqrt {2}x - 30 = 0$中,$a = 2$,$b=-\sqrt{2}$,$c = -30$。
计算判别式$\Delta=b^{2}-4ac=(-\sqrt{2})^{2}-4×2×(-30)=2 + 240 = 242$。
代入求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$得:
$x=\frac{\sqrt{2}\pm\sqrt{242}}{2×2}=\frac{\sqrt{2}\pm11\sqrt{2}}{4}$
即$x_1=\frac{\sqrt{2}+11\sqrt{2}}{4}=3\sqrt{2}$,$x_2=\frac{\sqrt{2}-11\sqrt{2}}{4}=-\frac{5\sqrt{2}}{2}$。
$(4)$ 解方程$\frac{1}{4}x^{2}-6x + 3 = 0$
解:方程两边同时乘以$4$化为一般形式$x^{2}-24x + 12 = 0$,此时$a = 1$,$b=-24$,$c = 12$。
计算判别式$\Delta=b^{2}-4ac=(-24)^{2}-4×1×12=576 - 48 = 528$。
代入求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$得:
$x=\frac{24\pm\sqrt{528}}{2}=\frac{24\pm4\sqrt{33}}{2}=12\pm2\sqrt{33}$
即$x_1=12 + 2\sqrt{33}$,$x_2=12 - 2\sqrt{33}$。
综上,$(1)$ $x_1=\frac{-3\sqrt{2}+\sqrt{21}}{3}$,$x_2=\frac{-3\sqrt{2}-\sqrt{21}}{3}$;$(2)$ $x_1=\frac{1+\sqrt{73}}{12}$,$x_2=\frac{1-\sqrt{73}}{12}$;$(3)$ $x_1=3\sqrt{2}$,$x_2=-\frac{5\sqrt{2}}{2}$;$(4)$ $x_1=12 + 2\sqrt{33}$,$x_2=12 - 2\sqrt{33}$。
8. 利用我们学过的完全平方公式及不等式知识能解决代数式一些问题。观察下列式子:
①$x^{2}+4x+2$
$=(x^{2}+4x+4)-2$
$=(x+2)^{2}-2$,
$\because (x+2)^{2}≥0$,
$\therefore x^{2}+4x+2=(x+2)^{2}-2≥-2$。
因此代数式$x^{2}+4x+2$有最小值-2;
②$-x^{2}+2x+3$
$=-(x^{2}-2x+1)+4$
$=-(x-1)^{2}+4$。
$\because -(x-1)^{2}≤0$,
$\therefore -x^{2}+2x+3=-(x-1)^{2}+4≤4$。
因此,代数式$-x^{2}+2x+3$有最大值4;
阅读上述材料并完成下列问题:
(1)代数式$-a^{2}-6a+4$的最大值为
(2)求代数式$a^{2}+b^{2}+4b-8a+11$的最小值;
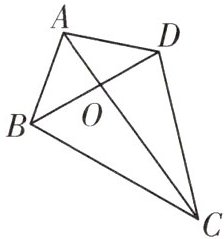
(3)如图,在四边形ABCD中,对角线AC,BD相交于点O,且$AC⊥BD$,若$AC+BD=12$,求四边形ABCD面积的最大值。
①$x^{2}+4x+2$
$=(x^{2}+4x+4)-2$
$=(x+2)^{2}-2$,
$\because (x+2)^{2}≥0$,
$\therefore x^{2}+4x+2=(x+2)^{2}-2≥-2$。
因此代数式$x^{2}+4x+2$有最小值-2;
②$-x^{2}+2x+3$
$=-(x^{2}-2x+1)+4$
$=-(x-1)^{2}+4$。
$\because -(x-1)^{2}≤0$,
$\therefore -x^{2}+2x+3=-(x-1)^{2}+4≤4$。
因此,代数式$-x^{2}+2x+3$有最大值4;
阅读上述材料并完成下列问题:
(1)代数式$-a^{2}-6a+4$的最大值为
13
;(2)求代数式$a^{2}+b^{2}+4b-8a+11$的最小值;
(3)如图,在四边形ABCD中,对角线AC,BD相交于点O,且$AC⊥BD$,若$AC+BD=12$,求四边形ABCD面积的最大值。

(2)原式$=a^{2}-8a+16+b^{2}+4b+4-9=(a-4)^{2}+(b+2)^{2}-9$,$\because (a-4)^{2}\geq0,(b+2)^{2}\geq0$,$\therefore a^{2}+b^{2}+4b-8a+11=(a-4)^{2}+(b+2)^{2}-9\geq-9$,$\therefore$代数式的最小值为-9;(3)$S_{四边形ABCD}=S_{\triangle ABD}+S_{\triangle BDC}=\frac{1}{2}BD× OA+\frac{1}{2}BD× OC=\frac{1}{2}BD(OA+OC)=\frac{1}{2}BD× AC$,设$BD=x$,则$AC=12-x$,$\therefore S_{四边形ABCD}=\frac{1}{2}x(12-x)=-\frac{1}{2}(x^{2}-12x)=-\frac{1}{2}[(x-6)^{2}-36]=-\frac{1}{2}(x-6)^{2}+18$,$\because -\frac{1}{2}(x-6)^{2}\leq0$,$\therefore S_{四边形ABCD}=-\frac{1}{2}(x-6)^{2}+18\leq18$,$\therefore$最大值为18。
答案:
解:
(1)原式$=-(a+3)^{2}+13$,$\because -(a+3)^{2}\leq0$,$\therefore -(a+3)^{2}+13\leq13$,$\therefore -a^{2}-6a+4$的最大值为13,故答案为:13;
(2)原式$=a^{2}-8a+16+b^{2}+4b+4-9=(a-4)^{2}+(b+2)^{2}-9$,$\because (a-4)^{2}\geq0,(b+2)^{2}\geq0$,$\therefore a^{2}+b^{2}+4b-8a+11=(a-4)^{2}+(b+2)^{2}-9\geq-9$,$\therefore$代数式的最小值为-9;
(3)$S_{四边形ABCD}=S_{\triangle ABD}+S_{\triangle BDC}=\frac{1}{2}BD\times OA+\frac{1}{2}BD\times OC=\frac{1}{2}BD(OA+OC)=\frac{1}{2}BD\times AC$,设$BD=x$,则$AC=12-x$,$\therefore S_{四边形ABCD}=\frac{1}{2}x(12-x)=-\frac{1}{2}(x^{2}-12x)=-\frac{1}{2}[(x-6)^{2}-36]=-\frac{1}{2}(x-6)^{2}+18$,$\because -\frac{1}{2}(x-6)^{2}\leq0$,$\therefore S_{四边形ABCD}=-\frac{1}{2}(x-6)^{2}+18\leq18$,$\therefore$最大值为18。
(1)原式$=-(a+3)^{2}+13$,$\because -(a+3)^{2}\leq0$,$\therefore -(a+3)^{2}+13\leq13$,$\therefore -a^{2}-6a+4$的最大值为13,故答案为:13;
(2)原式$=a^{2}-8a+16+b^{2}+4b+4-9=(a-4)^{2}+(b+2)^{2}-9$,$\because (a-4)^{2}\geq0,(b+2)^{2}\geq0$,$\therefore a^{2}+b^{2}+4b-8a+11=(a-4)^{2}+(b+2)^{2}-9\geq-9$,$\therefore$代数式的最小值为-9;
(3)$S_{四边形ABCD}=S_{\triangle ABD}+S_{\triangle BDC}=\frac{1}{2}BD\times OA+\frac{1}{2}BD\times OC=\frac{1}{2}BD(OA+OC)=\frac{1}{2}BD\times AC$,设$BD=x$,则$AC=12-x$,$\therefore S_{四边形ABCD}=\frac{1}{2}x(12-x)=-\frac{1}{2}(x^{2}-12x)=-\frac{1}{2}[(x-6)^{2}-36]=-\frac{1}{2}(x-6)^{2}+18$,$\because -\frac{1}{2}(x-6)^{2}\leq0$,$\therefore S_{四边形ABCD}=-\frac{1}{2}(x-6)^{2}+18\leq18$,$\therefore$最大值为18。
查看更多完整答案,请扫码查看


