A. 如果两个相似三角形对应高的比为4:5,那么这两个相似三角形的相似比是
4:5
,对应中线的比为4:5
,对应角平分线的比为4:5
。
答案:
4:5 4:5 4:5
B. 如图,已知∠1=∠B,则下列各式正确的是 (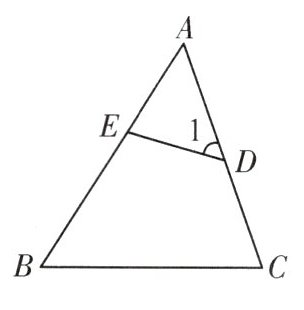
A.AD:BC=AE:EB
B.DE:BC=AD:AC
C.AD·AC=AE·AB
D.AC·AE=AD·AB
C
)
A.AD:BC=AE:EB
B.DE:BC=AD:AC
C.AD·AC=AE·AB
D.AC·AE=AD·AB
答案:
C
C. 在△ABC中,AD是高,矩形PQMN的顶点P,N分别在AB,AC上,QM在边BC上,若BC=8cm,AD=6cm,且PN=2PQ,则矩形PQMN的长和宽分别是多少?
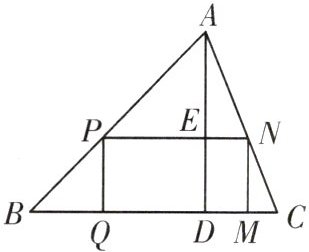
解:∵四边形PQMN为矩形,
∴PN//BC,
∴△APN∽△ABC,设宽PQ=xcm,则长PN=2xcm,DE=PQ=xcm,
∵AD=6cm,
∴AE=(6−x)cm,
∴$\frac{PN}{BC}=\frac{AE}{AD}$,
∵BC=8cm,
∴$\frac{2x}{8}=\frac{6−x}{6}$,
解得x=2.4,2x=4.8。
即长为4.8cm,宽为2.4cm。

解:∵四边形PQMN为矩形,
∴PN//BC,
∴△APN∽△ABC,设宽PQ=xcm,则长PN=2xcm,DE=PQ=xcm,
∵AD=6cm,
∴AE=(6−x)cm,
∴$\frac{PN}{BC}=\frac{AE}{AD}$,
∵BC=8cm,
∴$\frac{2x}{8}=\frac{6−x}{6}$,
解得x=2.4,2x=4.8。
即长为4.8cm,宽为2.4cm。
答案:
解:
∵四边形PQMN为矩形,
∴PN//BC,
∴△APN∽△ABC,设宽PQ=xcm,则长PN=2xcm,DE=PQ=xcm,
∵AD=6cm,
∴AE=(6−x)cm,
∴$\frac{PN}{BC}=\frac{AE}{AD}$,
∵BC=8cm,
∴______,
解得x=2.4,2x=4.8。
即长为4.8cm,宽为2.4cm。
答案:$\frac{2x}{8}=\frac{6−x}{6}$
∵四边形PQMN为矩形,
∴PN//BC,
∴△APN∽△ABC,设宽PQ=xcm,则长PN=2xcm,DE=PQ=xcm,
∵AD=6cm,
∴AE=(6−x)cm,
∴$\frac{PN}{BC}=\frac{AE}{AD}$,
∵BC=8cm,
∴______,
解得x=2.4,2x=4.8。
即长为4.8cm,宽为2.4cm。
答案:$\frac{2x}{8}=\frac{6−x}{6}$
1. 已知两个三角形对应边上的高的比为2:3,若已知较大三角形的一边中线长为4cm,则另一较小三角形的对应中线长为
$\frac{8}{3}$ cm
。
答案:
$\frac{8}{3}$ cm
2. 如图,已知△ACD∽△ADB,AC=4,AD=2,则AB的长为 (

A. 1
B. 2
C. 3
D. 4
A
)
A. 1
B. 2
C. 3
D. 4
答案:
A
3. 如图,在△ABC中,AD是高,矩形PQMN的顶点P,N分别在AB,AC上,QM在BC上,AD交PN于点E。设BC=48,AD=16,PQ:PN=5:9,求矩形PQMN的面积。

解:$\because PQ:PN=5:9$,
$\therefore$ 设 $PQ=5x$,则 $PN=9x$,
$\because$ 四边形 $PQMN$ 为矩形,
$\therefore ED=PQ=5x$,$AE=AD - DE=16 - 5x$。
又 $\because PN// BC$,
$\therefore \triangle APN\backsim\triangle ABC$,
$\therefore \frac{AE}{AD}=\frac{PN}{BC}$,即 $\frac{16 - 5x}{16}=\frac{9x}{48}$,解得 $x=$
$\therefore PQ=$
$\therefore S_{矩形PQMN}=PQ\cdot PN=10×18=$

解:$\because PQ:PN=5:9$,
$\therefore$ 设 $PQ=5x$,则 $PN=9x$,
$\because$ 四边形 $PQMN$ 为矩形,
$\therefore ED=PQ=5x$,$AE=AD - DE=16 - 5x$。
又 $\because PN// BC$,
$\therefore \triangle APN\backsim\triangle ABC$,
$\therefore \frac{AE}{AD}=\frac{PN}{BC}$,即 $\frac{16 - 5x}{16}=\frac{9x}{48}$,解得 $x=$
2
,$\therefore PQ=$
10
,$PN=$18
,$\therefore S_{矩形PQMN}=PQ\cdot PN=10×18=$
180
。
答案:
解:$\because PQ:PN=5:9$,
$\therefore$ 设 $PQ=5x$,则 $PN=9x$,
$\because$ 四边形 $PQMN$ 为矩形,
$\therefore ED=PQ=5x$,$AE=AD - DE=16 - 5x$。
又 $\because PN// BC$,
$\therefore \triangle APN\backsim\triangle ABC$,
$\therefore \frac{AE}{AD}=\frac{PN}{BC}$,即 $\frac{16 - 5x}{16}=\frac{9x}{48}$,解得 $x=2$,
$\therefore PQ=10$,$PN=18$,
$\therefore S_{矩形PQMN}=PQ\cdot PN=10\times18=180$。
$\therefore$ 设 $PQ=5x$,则 $PN=9x$,
$\because$ 四边形 $PQMN$ 为矩形,
$\therefore ED=PQ=5x$,$AE=AD - DE=16 - 5x$。
又 $\because PN// BC$,
$\therefore \triangle APN\backsim\triangle ABC$,
$\therefore \frac{AE}{AD}=\frac{PN}{BC}$,即 $\frac{16 - 5x}{16}=\frac{9x}{48}$,解得 $x=2$,
$\therefore PQ=10$,$PN=18$,
$\therefore S_{矩形PQMN}=PQ\cdot PN=10\times18=180$。
查看更多完整答案,请扫码查看


