《2025年春如金卷课时作业AB本九年级数学上册北师大版》

3. 甲、乙、丙三人中任选两人参加志愿者服务活动,则甲被选中的概率为（D）
A. $\frac {1}{3}$
B. $\frac {1}{5}$
C. $\frac {5}{6}$
D. $\frac {2}{3}$

答案： D

4. 甲、乙、丙、丁4人聚会,每人带了一件礼物,4件礼物外盒包装完全相同,将4件礼物放在一起。甲先从中随机抽取一件,不放回,乙再从中随机抽取一件,求甲、乙两人抽到的都不是自己带来的礼物的概率。

答案：
解：设甲、乙、丙、丁4人的礼物分别记为a，b，c，d，根据题意画树状图如下： 共有12种等可能的结果，甲、乙两人抽到的都不是自己带来的礼物的结果有7个，
∴甲、乙两人抽到的都不是自己带来的礼物的概率为$\frac{7}{12}$。

5. 一个不透明的盒子里有4个除颜色外其他完全相同的小球,其中每个小球上分别标有1,-1,-2,-3四个不同的数字,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下数字后再放回盒子,求两次摸出的小球上数字乘积是负数的概率。

答案：
解：画树状图得：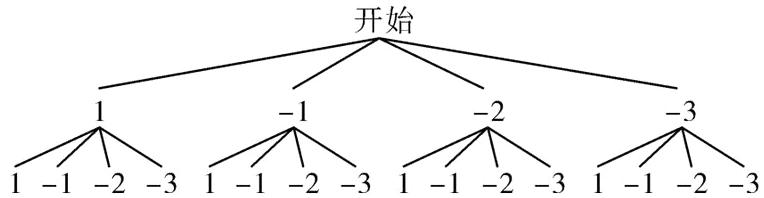

∵共有16种等可能的结果，两次摸出的小球上数字乘积是负数的有6种情况，
∴两次摸出的小球上数字乘积是负数的概率为：$\frac{6}{16}=\frac{3}{8}$。

6. 一个不透明的口袋中装有4个分别标有数字-1,-2,3,4的小球,它们的形状、大小完全相同。小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y。
(1)请用列表法或画树状图的方法表示出由x,y确定的点$P(x,y)$所有可能的结果;
(2)若规定:点$P(x,y)$在第一象限或第三象限小红获胜;点$P(x,y)$在第二象限或第四象限则小颖获胜.这个游戏是否公平,请说明理由。

答案：
(1)列表如下：| | -1 | -2 | 3 | 4 | | --- | --- | --- | --- | --- | | -1 | | (-1,-2) | (-1,3) | (-1,4) | | -2 | (-2,-1) | | (-2,3) | (-2,4) | | 3 | (3,-1) | (3,-2) | | (3,4) | | 4 | (4,-1) | (4,-2) | (4,3) | |
(2)从上面的表格可以看出，所有可能出现的结果共有12种，且每种结果出现的可能性相同，其中点$(x,y)$在第一象限或第三象限的结果有4种，第二象限或第四象限的结果有8种，所以小红获胜的概率$=\frac{4}{12}=\frac{1}{3}$，小颖获胜的概率$=\frac{8}{12}=\frac{2}{3}$，
∵$\frac{1}{3}≠\frac{2}{3}$，这个游戏不公平。