11. 如图,一次函数$y=k_{1}x+b$的图象经过$A(0,-2)$,$B(1,0)$两点,与反比例函数$y=\frac{k_{2}}{x}$的图象在第一象限内的交点为$M(m,4)$。
(1)求一次函数和反比例函数的解析式;
(2)点$C$是线段$AM$上一点,若$S_{\triangle OCM}=\frac{1}{3}S_{\triangle AMO}$,求点$C$的坐标。
(1)一次函数的解析式为
(2)点$C$的坐标为
(1)求一次函数和反比例函数的解析式;
(2)点$C$是线段$AM$上一点,若$S_{\triangle OCM}=\frac{1}{3}S_{\triangle AMO}$,求点$C$的坐标。
(1)一次函数的解析式为
$y=2x-2$
,反比例函数的解析式为$y=\frac{12}{x}$
。(2)点$C$的坐标为
$(2,2)$
。
答案:
解:
(1)将$A(0,-2)$,$B(1,0)$代入$y = k_1x + b$,得$\begin{cases}b = -2\\k_1 + b = 0\end{cases}$解得$k_1 = 2$,$b = -2$。所以一次函数的解析式为$y = 2x - 2$。将$M(m,4)$代入$y = 2x - 2$中,得$4 = 2m - 2$。解得$m = 3$。所以点$M$的坐标为$(3,4)$。因为反比例函数$y = \frac{k_2}{x}$的图象过点$M(3,4)$,得$4 = \frac{k_2}{3}$。解得$k_2 = 12$。所以反比例函数的解析式为$y = \frac{12}{x}$。
(2)根据题意,得$S_{\triangle AMO} = \frac{1}{2}×2×3 = 3$。则$S_{\triangle OCM} = \frac{1}{3}S_{\triangle AMO} = 1$。可得$S_{\triangle AOC} = S_{\triangle AMO} - S_{\triangle OCM} = 3 - 1 = 2$。由$OA = 2$可知点$C$的横坐标为$2$。将$x = 2$代入$y = 2x - 2$中,得$y = 2$。所以点$C$的坐标为$(2,2)$。
(1)将$A(0,-2)$,$B(1,0)$代入$y = k_1x + b$,得$\begin{cases}b = -2\\k_1 + b = 0\end{cases}$解得$k_1 = 2$,$b = -2$。所以一次函数的解析式为$y = 2x - 2$。将$M(m,4)$代入$y = 2x - 2$中,得$4 = 2m - 2$。解得$m = 3$。所以点$M$的坐标为$(3,4)$。因为反比例函数$y = \frac{k_2}{x}$的图象过点$M(3,4)$,得$4 = \frac{k_2}{3}$。解得$k_2 = 12$。所以反比例函数的解析式为$y = \frac{12}{x}$。
(2)根据题意,得$S_{\triangle AMO} = \frac{1}{2}×2×3 = 3$。则$S_{\triangle OCM} = \frac{1}{3}S_{\triangle AMO} = 1$。可得$S_{\triangle AOC} = S_{\triangle AMO} - S_{\triangle OCM} = 3 - 1 = 2$。由$OA = 2$可知点$C$的横坐标为$2$。将$x = 2$代入$y = 2x - 2$中,得$y = 2$。所以点$C$的坐标为$(2,2)$。
12. 某疫苗生产企业月生产数量$y$(万支)与月份$x$之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分,请根据图中数据解答下列问题:
(1)该企业4月份的生产数量为
(2)该企业有
(1)该企业4月份的生产数量为
45
万支?(2)该企业有
6
个月的月生产数量不超过90万支?
答案:
解:
(1)当$1\leq x\leq4$时,设$y$与$x$的函数关系式为$y = \frac{k}{x}$,
∵点$(1,180)$在该函数图象上,
∴$180 = \frac{k}{1}$,得$k = 180$,
∴$y = \frac{180}{x}$,当$x = 4$时,$y = \frac{180}{4} = 45$,即该疫苗生产企业4月份的生产数量为45万支;
(2)设技术改造完成后对应的函数解析式为$y = ax + b$,
∵点$(4,45)$,$(5,60)$在该函数图象上,
∴$\begin{cases}4a + b = 45\\5a + b = 60\end{cases}$,解得$\begin{cases}a = 15\\b = -15\end{cases}$,
∴技术改造完成后对应的函数解析式为$y = 15x - 15$,由题意得$\begin{cases}\frac{180}{x}\leq90\\15x - 15\leq90\end{cases}$解得$2\leq x\leq7$,经检验符合题意,
∵$x$为正整数,
∴$x = 2,3,4,5,6,7$,答:该疫苗生产企业有6个月的月生产数量不超过90万支。
(1)当$1\leq x\leq4$时,设$y$与$x$的函数关系式为$y = \frac{k}{x}$,
∵点$(1,180)$在该函数图象上,
∴$180 = \frac{k}{1}$,得$k = 180$,
∴$y = \frac{180}{x}$,当$x = 4$时,$y = \frac{180}{4} = 45$,即该疫苗生产企业4月份的生产数量为45万支;
(2)设技术改造完成后对应的函数解析式为$y = ax + b$,
∵点$(4,45)$,$(5,60)$在该函数图象上,
∴$\begin{cases}4a + b = 45\\5a + b = 60\end{cases}$,解得$\begin{cases}a = 15\\b = -15\end{cases}$,
∴技术改造完成后对应的函数解析式为$y = 15x - 15$,由题意得$\begin{cases}\frac{180}{x}\leq90\\15x - 15\leq90\end{cases}$解得$2\leq x\leq7$,经检验符合题意,
∵$x$为正整数,
∴$x = 2,3,4,5,6,7$,答:该疫苗生产企业有6个月的月生产数量不超过90万支。
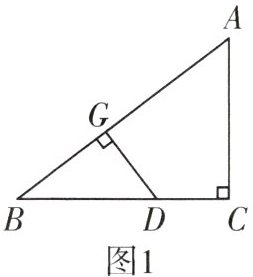
13. 如图1,在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$AC=3$,$BC=4$,动点$D$从点$B$出发,沿着折线$B\to C\to A$(含端点)运动,速度为每秒1个单位长度,到达$A$点停止运动。设点$D$的运动时间为$t$,点$D$到$AB$的距离$DG$为$y_{1}$,请解答下列问题:
(1)直接写出$y_{1}$关于$t$的函数关系式,并写出$t$的取值范围;
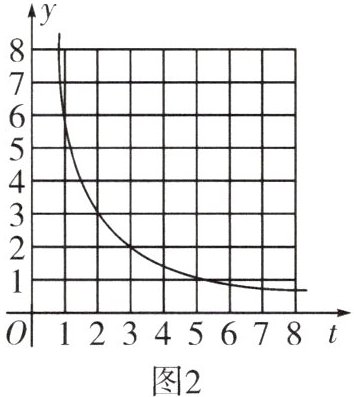
(2)在图2的直角坐标系中画出(1)中$y_{1}$关于$t$的图象,并写出该函数的一条性质;
(3)若函数$y_{2}=\frac{6}{t}(t>0)$的图象如图2所示,结合函数图象,直接估计当$y_{1}\leqslant y_{2}$时$t$的取值范围。(保留1位小数,误差不超过0.2)
(1)直接写出$y_{1}$关于$t$的函数关系式,并写出$t$的取值范围;
(2)在图2的直角坐标系中画出(1)中$y_{1}$关于$t$的图象,并写出该函数的一条性质;
(3)若函数$y_{2}=\frac{6}{t}(t>0)$的图象如图2所示,结合函数图象,直接估计当$y_{1}\leqslant y_{2}$时$t$的取值范围。(保留1位小数,误差不超过0.2)


答案:
解:
(1)
∵$\angle C = 90^{\circ}$,$AC = 3$,$BC = 4$,
∴$AB = \sqrt{AC^2 + BC^2} = \sqrt{3^2 + 4^2} = 5$,当点$D$在线段$BC$上,如图1.1,$0\leq t\leq4$,$BD = t$,
∵$\angle DGB = \angle ACB = 90^{\circ}$,$\angle B = \angle B$,
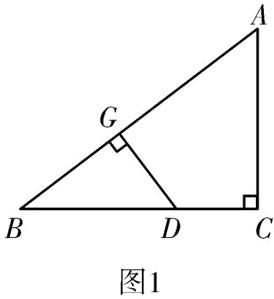
∴$\triangle DGB\sim\triangle ACB$,
∴$\frac{DG}{AC} = \frac{BD}{AB}$,
∴$\frac{y}{3} = \frac{t}{5}$,
∴$y = \frac{3}{5}t$;当点$D$在线段$AC$上,如图1.2,$4\lt t\leq7$,$AD = 7 - t$,
∵$\angle DGA = \angle ACB = 90^{\circ}$,$\angle A = \angle A$,
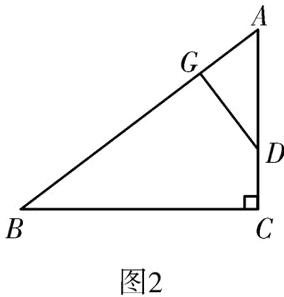
∴$\triangle DGA\sim\triangle BCA$,
∴$\frac{DG}{BC} = \frac{AD}{AB}$,
∴$\frac{y}{4} = \frac{7 - t}{5}$,
∴$y = -\frac{4}{5}t + \frac{28}{5}$;综上,$y = \begin{cases}\frac{3}{5}t(0\leq t\leq4)\\-\frac{4}{5}t + \frac{28}{5}(4\lt t\leq7)\end{cases}$;
(2)列表得:
t 0 4 7
y 0 2.4 0
在图2的直角坐标系中画出$y$的图象,如图3:

由图可得,当$0\leq x\leq4$时,$y$的值随着$x$的增大而增大,当$4\lt x\leq7$时,$y$的值随着$x$的增大而减小;
(3)函数$y_2 = \frac{6}{t}(t\gt0)$的图象如图2,由图可知:当$y_1\leq y_2$时,表明函数的图象在$y_1$的图象上方或两者的相交位置,由图象可知此时$0\lt t\leq3.2$或$5.7\leq t\leq7$。
解:
(1)
∵$\angle C = 90^{\circ}$,$AC = 3$,$BC = 4$,
∴$AB = \sqrt{AC^2 + BC^2} = \sqrt{3^2 + 4^2} = 5$,当点$D$在线段$BC$上,如图1.1,$0\leq t\leq4$,$BD = t$,
∵$\angle DGB = \angle ACB = 90^{\circ}$,$\angle B = \angle B$,

∴$\triangle DGB\sim\triangle ACB$,
∴$\frac{DG}{AC} = \frac{BD}{AB}$,
∴$\frac{y}{3} = \frac{t}{5}$,
∴$y = \frac{3}{5}t$;当点$D$在线段$AC$上,如图1.2,$4\lt t\leq7$,$AD = 7 - t$,
∵$\angle DGA = \angle ACB = 90^{\circ}$,$\angle A = \angle A$,

∴$\triangle DGA\sim\triangle BCA$,
∴$\frac{DG}{BC} = \frac{AD}{AB}$,
∴$\frac{y}{4} = \frac{7 - t}{5}$,
∴$y = -\frac{4}{5}t + \frac{28}{5}$;综上,$y = \begin{cases}\frac{3}{5}t(0\leq t\leq4)\\-\frac{4}{5}t + \frac{28}{5}(4\lt t\leq7)\end{cases}$;
(2)列表得:
t 0 4 7
y 0 2.4 0
在图2的直角坐标系中画出$y$的图象,如图3:

由图可得,当$0\leq x\leq4$时,$y$的值随着$x$的增大而增大,当$4\lt x\leq7$时,$y$的值随着$x$的增大而减小;
(3)函数$y_2 = \frac{6}{t}(t\gt0)$的图象如图2,由图可知:当$y_1\leq y_2$时,表明函数的图象在$y_1$的图象上方或两者的相交位置,由图象可知此时$0\lt t\leq3.2$或$5.7\leq t\leq7$。
查看更多完整答案,请扫码查看


