A. 如图,找出下列位似图形的位似中心。
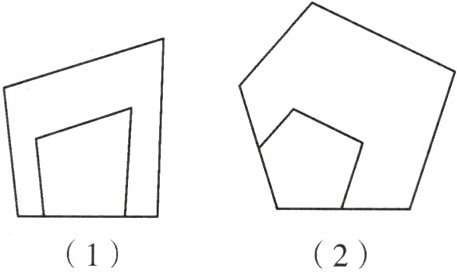
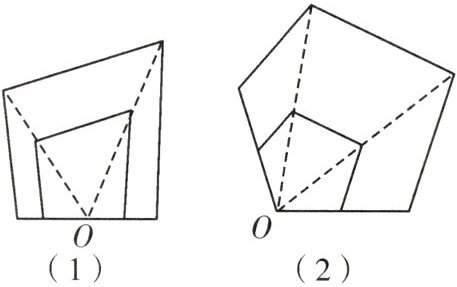


点O就是所求的位似中心。
答案:
【解析】:根据位似中心的定义,位似中心是位似图形对应顶点连线的交点。对于这两个位似图形,通过连接对应顶点并延长,其交点即为位似中心。
【答案】:点$O$就是所求的位似中心。
【解析】:根据位似中心的定义,位似中心是位似图形对应顶点连线的交点。对于这两个位似图形,通过连接对应顶点并延长,其交点即为位似中心。
【答案】:点$O$就是所求的位似中心。

B. 如图,$\triangle ABC$与$\triangle DEF$是位似图形,点O是位似中心,$OA=AD$,则$\triangle ABC$与$\triangle DEF$的相似比是(
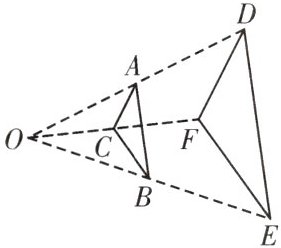
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.2
D.3
A
)
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.2
D.3
答案:
A
C. 如图,四边形ABCD各顶点的坐标分别为$A(2,6)$,$B(4,2)$,$C(6,2)$,$D(6,4)$,在第一象限内画出以原点O为位似中心,相似比为$\frac{1}{2}$的位似图形$A_1B_1C_1D_1$,并写出各点坐标。

$A_1$(

$A_1$(
1
,3
),$B_1$(2
,1
),$C_1$(3
,1
),$D_1$(3
,2
)。
答案:
解:如图可知:
$A_1(1,3)$,
$B_1(2,1)$,
$C_1(3,1)$,
$D_1(3,2)$。
$A_1(1,3)$,
$B_1(2,1)$,
$C_1(3,1)$,
$D_1(3,2)$。
1. 如图,在$\triangle ABC$中,已知$DE // BC$。
(1)$\triangle ADE$与$\triangle ABC$相似吗?为什么?
(2)它们是位似图形吗?如果是,请指出位似中心。

(1)$\triangle ADE$与$\triangle ABC$相似吗?为什么?
$\triangle ADE$与$\triangle ABC$相似。因为$DE// BC$,所以$\triangle ADE\backsim \triangle ABC$。
(2)它们是位似图形吗?如果是,请指出位似中心。
是位似图形,位似中心是点$A$。

答案:
解:
(1)$\triangle ADE$与$\triangle ABC$相似。
$\because DE// BC$,
$\therefore \triangle ADE\backsim \triangle ABC$。
(2)是位似图形。由
(1)知:$\triangle ADE\backsim \triangle ABC$。
$\because \triangle ADE$和$\triangle ABC$的对应顶点的连线$BD$,$CE$相交于点$A$,
$\therefore \triangle ADE$和$\triangle ABC$是位似图形,位似中心是点$A$。
(1)$\triangle ADE$与$\triangle ABC$相似。
$\because DE// BC$,
$\therefore \triangle ADE\backsim \triangle ABC$。
(2)是位似图形。由
(1)知:$\triangle ADE\backsim \triangle ABC$。
$\because \triangle ADE$和$\triangle ABC$的对应顶点的连线$BD$,$CE$相交于点$A$,
$\therefore \triangle ADE$和$\triangle ABC$是位似图形,位似中心是点$A$。
2. 如图,$\triangle ABC$和$\triangle A'B'C'$是位似图形,且$OA'=\frac{3}{2}OA$,则$AB:A'B'$等于(
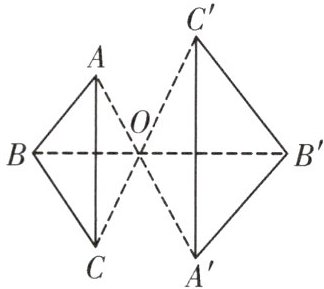
A. $3:2$
B. $2:3$
C. $3:5$
D. $5:3$
B
)
A. $3:2$
B. $2:3$
C. $3:5$
D. $5:3$
答案:
B
3. 将图中的$\triangle ABC$以点B为位似中心,放大到原来的2倍。


答案:
解:如图所示:

解:如图所示:

查看更多完整答案,请扫码查看


