《2024年高职高考全真模拟试卷辽海出版社高中数学全一册人教版》

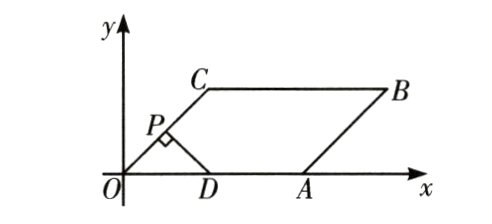
22. 如图，在平面直角坐标系xOy中，四边形OABC为平行四边形，点A(4, 0)，∠AOC = $\frac{\pi}{4}$
(1)若|OC| = 2，求点C的坐标；
(2)设|OC| = 2m，点P为线段OC的中点，OC的中垂线交x轴于点D，记三角形ODP的面积为S₁，平行四边形的面积为S₂，若S₂ = 4S₁，则求m的值.

答案： 解：
(1)设$C$坐标为$(a,b)(a ＞ 0,b ＞ 0)$，
$\because|OC| = 2$，$\angle AOC=\frac{\pi}{4}$
$\therefore a = b$，且$a^{2}+b^{2}=|OC|^{2}$
$\therefore2a^{2}=4$，解得：$a = b=\sqrt{2}$，$\therefore C(\sqrt{2},\sqrt{2})$
(2)已知点$A(4,0)$，$\therefore|AO| = 4$
又$|OC| = 2m$，$\angle AOC=\frac{\pi}{4}$，
$\therefore S_{2}=|AO|\cdot|OC|\cdot\sin\frac{\pi}{4}=4\sqrt{2}m$，
又$OC\perp DP$，$\therefore\angle ODP=\angle AOC=\frac{\pi}{4}$，且$P$为$OC$中点，所以$OP = DP = m$，
$\therefore S_{1}=\frac{1}{2}\cdot|OP|\cdot|DP|=\frac{1}{2}\cdot m\cdot m=\frac{m^{2}}{2}$，
令$4S_{1}=S_{2}$，即：$4\times\frac{m^{2}}{2}=4\sqrt{2}m$，
$\therefore m^{2}=2\sqrt{2}m$，解得：$m = 2\sqrt{2}$

23. 已知等差数列{aₙ}中，a₁ = -2，a₁₂ = 20
(1)求{aₙ}的通项公式aₙ；
(2)令bₙ = $\frac{a₁ + a₂ + a₃ + \cdots + aₙ}{n}$，求数列{3ᵇₙ}的前n项和Tₙ.

答案： 解：
(1)设等差数列$\{a_{n}\}$的公差为$d$，
已知：$a_{1}=-2$，$a_{12}=20$，由$a_{12}=a_{1}+11d$得：$20=-2 + 11d$，解得：$d = 2$，
$\therefore a_{n}=a_{1}+(n - 1)d=-2+(n - 1)\times2=2n - 4(n\in\mathbf{N}_{+})$
(2)由
(1)知：$a_{n}=2n - 4$，
$\therefore a_{1}+a_{2}+a_{3}+\cdots+a_{n}=\frac{(a_{1}+a_{n})n}{2}=(n - 3)n$
$\therefore b_{n}=\frac{(n - 3)n}{n}=n - 3$
$\therefore T_{n}=3^{b_{1}}+3^{b_{2}}+3^{b_{3}}+\cdots+3^{b_{n}}$
$=3^{-2}+3^{-1}+3^{0}+\cdots+3^{n - 3}$
$=\frac{3^{-2}(1 - 3^{n})}{1 - 3}=\frac{1}{2}\cdot3^{n - 2}-\frac{1}{18}(n\in\mathbf{N}^{+})$