《2024年高职高考全真模拟试卷辽海出版社高中数学全一册人教版》

12. 已知sinα = $\frac{2}{3}$，则cos(π - 2α) = ( )
A. $\frac{\sqrt{5}}{3}$
B. - $\frac{\sqrt{5}}{3}$
C. $\frac{1}{9}$
D. - $\frac{1}{9}$

答案： D

13. 已知函数y = aˣ是函数f(x)的反函数，且f(x)过点(8，3)，则a = ( )
A. 2
B. 3
C. 4
D. 8

答案： A

14. O为坐标原点，F为抛物线C：y² = 4$\sqrt{2}$x的焦点，P为C上一点，若|PF| = 4$\sqrt{2}$，则△POF的面积为( )
A. - 2
B. 2
C. 2$\sqrt{3}$
D. 4

答案： C

15. 若圆心在x轴上、半径为$\sqrt{5}$的圆C位于y轴左侧，且与直线x + 2y = 0相切，则圆C的方程是 ( )
A. (x - $\sqrt{5}$)² + y² = 5
B. (x + $\sqrt{5}$)² + y² = 5
C. (x - 5)² + y² = 5
D. (x + 5)² + y² = 5

答案： D

16. 某同学从学校开设的“手工”“茶艺”“魔方”“网球”“足球”“滑板”“围棋”“象棋”这8门课程中任选一门，则选到棋类课程的概率为________.

答案： $\frac{1}{4}$

17. 等差数列{aₙ}中，d = 2，且a₁，a₃，a₄成等比数列，则a₂ = ________.

答案： -6

18. 若向量$\boldsymbol{a}$ = (2，1)，$\boldsymbol{b}$ = (1，3)，$\boldsymbol{c}$ = (x，5)，且(2$\boldsymbol{a}$ + $\boldsymbol{b}$)·$\boldsymbol{c}$ = 25，则x = ________.

答案： 0

19. 已知样本数据x₁，x₂，…，x₁₀，其中x₁，x₂，x₃的平均数为a，x₄，x₅，…，x₁₀的平均数为b，则样本数据的平均数为________

答案： $\frac{3a + 7b}{10}$

20. 若直线x - 2y + 5 = 0与直线2x + my - 6 = 0互相垂直，则实数m = ________.

答案： 1

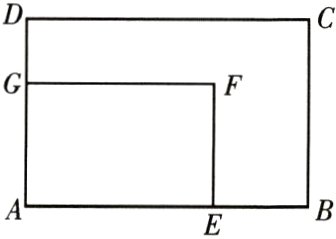
21. 如图，现有一块AB = 8 m，AD = 6 m的矩形空地ABCD，要改造成一个矩形AEFG花坛，其余为草坪的绿化带，设EB = 2x m，GD = x m.
(1)求矩形花坛的面积y与x的解析式；
(2)当x为何值时，花坛面积是草坪面积的一半.

答案： 解：
(1)$\because AB = 8$，$AD = 6$，$EB = 2x$，$GD = x$
$\therefore AG = 6 - x$，$AE = 8 - 2x$
$\therefore y = (6 - x)(8 - 2x) = 2x^{2} - 20x + 48(0 ＜ x ＜ 4)$
(2)$S_{ABCD} = AB\cdot AD = 48$
草坪面积 $= S_{ABCD} - S_{AEFG} = 48 - (2x^{2} - 20x + 48) = -2x^{2} + 20x$
$\because$ 花坛面积是草坪面积的一半
$\therefore 2x^{2} - 20x + 48 = \frac{1}{2}(-2x^{2} + 20x)$
即 $x^{2} - 10x + 16 = 0$
解得 $x = 2$ 或 $x = 8$(舍去)
$\therefore$ 当 $x = 2$ 时，花坛面积是草坪面积的一半