《2025年学习质量监测数学选择性必修第二册人教A版》

1. 已知数列$\sqrt{2},\sqrt{5},2\sqrt{2},\cdots$，则$2\sqrt{5}$是该数列的( )．
（A）第5项 （B）第6项
（C）第7项 （D）第8项

答案： C

2. 在数列$\{ a_{n}\}$中，$a_{1}=\frac{1}{3}$，$a_{n}=(-1)^{n}\cdot 2a_{n - 1}(n\geqslant2)$，则$a_{5}$的值为( )．
（A）$-\frac{16}{3}$ （B）$\frac{16}{3}$ （C）$-\frac{8}{3}$ （D）$\frac{8}{3}$

答案： B

3. 在数列$\{ a_{n}\}$中，$a_{n + 1}=a_{n}+3$，则数列$\{ a_{n}\}$为( )．
（A）递增数列 （B）递减数列
（C）常数列 （D）不具有单调性的数列

答案： A

4. 数列$1,3,6,10,15,\cdots$的递推公式可以为( )．
（A）$\begin{cases}a_{1}=1,\\a_{n + 1}=a_{n}+n,n\in\mathbf{N}^{*}\end{cases}$ （B）$\begin{cases}a_{1}=1,\\a_{n}=a_{n - 1}+n,n\geqslant2\end{cases}$
（C）$\begin{cases}a_{1}=1,\\a_{n + 1}=a_{n}+n - 1,n\in\mathbf{N}^{*}\end{cases}$ （D）$\begin{cases}a_{1}=1,\\a_{n}=a_{n - 1}+n - 1,n\geqslant2\end{cases}$

答案： B

5. 在数列$\{ a_{n}\}$中，$a_{1}=-\frac{1}{4}$，$a_{n}=1-\frac{1}{a_{n - 1}}(n\geqslant2)$，则$a_{2024}$的值为( )．
（A）$-\frac{1}{4}$ （B）5 （C）$\frac{4}{5}$ （D）以上都不对

答案： B

6. 已知数列$\{ a_{n}\}$的前n项和为$S_{n}=n^{2}$，则$S_{5}=$__________，$S_{4}=$__________，$a_{5}=$__________．

答案： 25；16；9

7. 已知数列$\{ a_{n}\}$的前n项和为$S_{n}=\frac{n}{n + 1}$，则$\frac{1}{a_{5}}=$________．

答案： 30

8. 根据下面的图形及相应的点数，写出点数构成的数列的一个通项公式为$a_{n}=$__________．

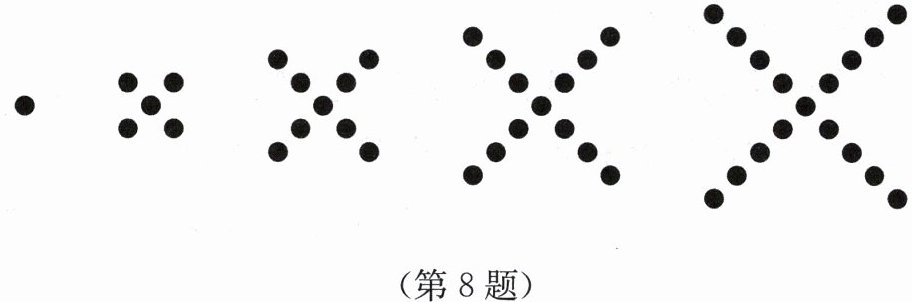
答案： $4n - 3$

9. 设数列$\{ a_{n}\}$的前n项和为$S_{n}$，且$\forall n\in\mathbf{N}^{*}$，$a_{n + 1}＞a_{n}$，$S_{n}\geqslant S_{6}$．请写出一个满足条件的数列$\{ a_{n}\}$的通项公式$a_{n}=$________．

答案： $n - 6$（答案不唯一）