《2025年学习质量监测数学选择性必修第二册人教A版》

11. 用导数的定义求函数$y = -\sqrt{x}$在$x = 1$处的导数，以及该曲线在点$(1, -1)$处的切线方程.

答案： 解：$\because\Delta y=\frac{1}{\sqrt{1+\Delta x}}-1=\frac{1-\sqrt{1+\Delta x}}{\sqrt{1+\Delta x}}=\frac{-\Delta x}{\sqrt{1+\Delta x}(1+\sqrt{1+\Delta x})}$，
$\therefore\frac{\Delta y}{\Delta x}=\frac{-1}{\sqrt{1+\Delta x}(1+\sqrt{1+\Delta x})}$，
$\therefore\lim\limits_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=-\frac{1}{2}$，即$y^{\prime}\vert_{x = 1}=-\frac{1}{2}$，
$\therefore$该曲线在点$(1,1)$处的切线方程是$x + 2y - 3 = 0$。

12. 已知函数$f(x)=ax^2 + 1(a\gt0)$，$g(x)=x^3 + bx$. 若曲线$y = f(x)$与曲线$y = g(x)$在它们的交点$(1,c)$处具有公切线，求$a,b$的值.

答案： 解：$\because f^{\prime}(1)=\lim\limits_{\Delta x \to 0}\frac{a(1+\Delta x)^{2}+1-(a + 1)}{\Delta x}=2a$，
$\therefore$切线斜率$k_{1}=2a$。
同理可得，$k_{2}=g^{\prime}(1)=3 + b$。
$\because$在交点$(1,c)$处有公切线，$\therefore 2a = 3 + b$。
又$\because c = a + 1$，且$c = 1 + b$，
$\therefore a = b$。由$\begin{cases}2a = 3 + b\\a = b\end{cases}$，得$\begin{cases}a = 3\\b = 3\end{cases}$。

1. 已知函数$y = f(x)$，若$f(1)=f'(1)=-1$，则函数$f(x)$的图象在点$(1,f(1))$附近的大致形状为( ).

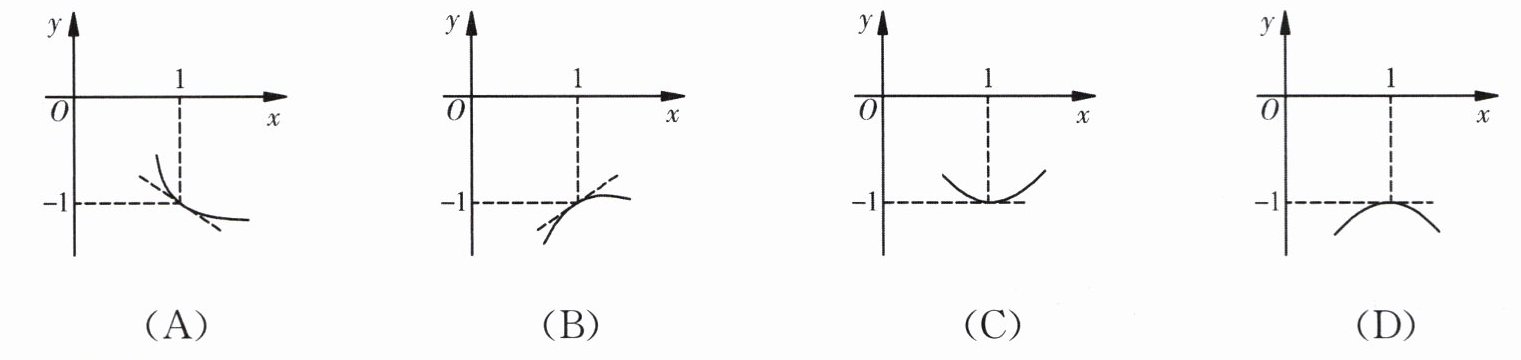
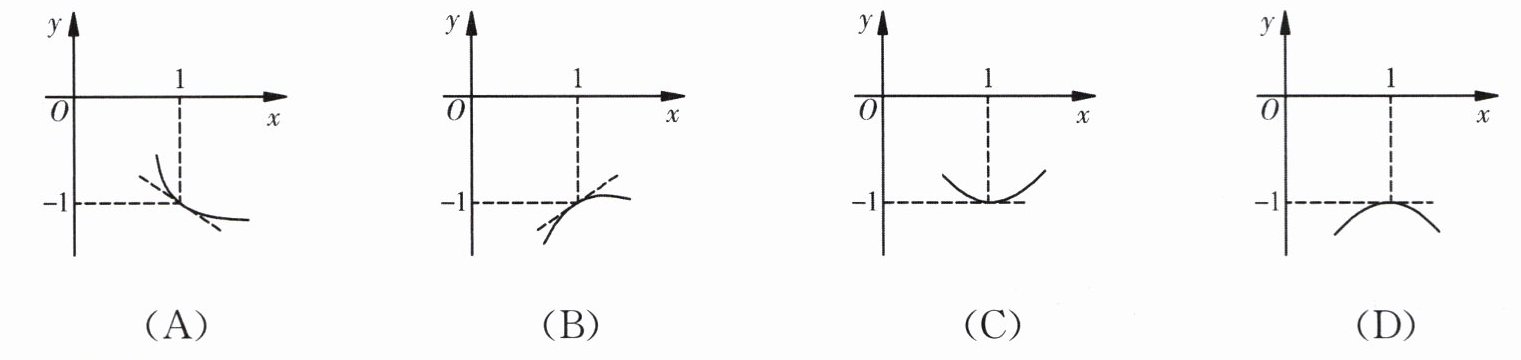
答案： A

2. 下列命题正确的是( ).
(A)若$f'(x_0)=0$，则曲线$f(x)$在$x = x_0$处无切线
(B)曲线$y = f(x)$的切线与该曲线可以有两个公共点
(C)曲线$y = f(x)$在$x = 1$处的切线方程为$2x - y = 0$，则当$\Delta x\to0$时，$\frac{f(1)-f(1+\Delta x)}{2\Delta x}=1$
(D)若函数$f(x)$的导数$f'(x)=2x^2 - 1$，且$f(1)=2$，则$f(x)$的图象在$x = 1$处的切线方程为$x + y - 3 = 0$

答案： B [提示]曲线$y = f(x)$的切线与该曲线可以有两个公共点，例如函数$f(x)=x^{3}-3x$，曲线$y = f(x)$在$x = 1$处的切线方程为$y = - 2$，与函数的图象还有一个公共点$(-2,-2)$，故选项B正确。

3. 函数$f(x)$的图象如图所示，设$f'(x)$是$f(x)$的导函数，则$f'(x_A)$与$f'(x_B)$的大小关系是_______.

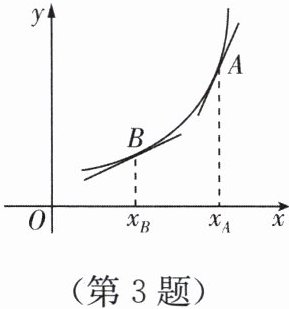
答案： $f^{\prime}(x_{A})＞f^{\prime}(x_{B})$ [提示]根据函数在某点处的导数的几何意义，结合图象可以判断。