2025年学习质量监测数学选择性必修第二册人教A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学习质量监测数学选择性必修第二册人教A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 曲线$y = - 2x^{2}+1$在点$(0,1)$处的切线的斜率是( ).
(A)-4 (B)0 (C)4 (D)不存在
(A)-4 (B)0 (C)4 (D)不存在
答案:
B
2. 已知函数$f(x)$在$x = x_{0}$处的导数为$f'(x_{0})$,则$\lim\limits_{\Delta x\rightarrow0}\frac{f(x_{0}+3\Delta x)-f(x_{0})}{\Delta x}=( )$.
(A)$-\frac{1}{3}f'(x_{0})$ (B)$-3f'(x_{0})$ (C)$3f'(x_{0})$ (D)$\frac{1}{3}f'(x_{0})$
(A)$-\frac{1}{3}f'(x_{0})$ (B)$-3f'(x_{0})$ (C)$3f'(x_{0})$ (D)$\frac{1}{3}f'(x_{0})$
答案:
C
3. 曲线$y = -\frac{1}{x}$在点$(\frac{1}{2},-2)$处的切线方程是( ).
(A)$y = 4x$ (B)$y = - 4x - 4$ (C)$y = 4x - 4$ (D)$y = 2x - 4$
(A)$y = 4x$ (B)$y = - 4x - 4$ (C)$y = 4x - 4$ (D)$y = 2x - 4$
答案:
C
4. 若函数$f(x)$在$x_{0}$处可导,则对$\lim\limits_{h\rightarrow0}\frac{f(x_{0}+h)-f(x_{0})}{h}$的结果表述正确的是( ).
(A)与$x_{0},h$均无关 (B)仅与$x_{0}$有关,而与$h$无关
(C)仅与$h$有关,而与$x_{0}$无关 (D)与$x_{0},h$均有关
(A)与$x_{0},h$均无关 (B)仅与$x_{0}$有关,而与$h$无关
(C)仅与$h$有关,而与$x_{0}$无关 (D)与$x_{0},h$均有关
答案:
B
5. 函数$f(x)$的图象如图所示,下列排序正确的是( ).
(A)$f'(1)>f'(2)>f'(3)>0$
(B)$f'(1)<f'(2)<f'(3)<0$
(C)$0<f'(1)<f'(2)<f'(3)$
(D)$f'(1)>f'(2)>0>f'(3)$
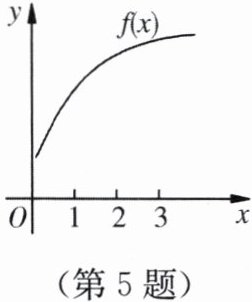
(A)$f'(1)>f'(2)>f'(3)>0$
(B)$f'(1)<f'(2)<f'(3)<0$
(C)$0<f'(1)<f'(2)<f'(3)$
(D)$f'(1)>f'(2)>0>f'(3)$

答案:
A
6. 若曲线$y = f(x)$在$x = x_{0}$处的切线方程为$3x + y - 1 = 0$,则$f'(x_{0})=$_______.
答案:
-3
7. 曲线$f(x)=\sqrt{x}$在点$(4,2)$处的切线的斜率是_________.
答案:
$\frac{1}{4}$
8. 曲线$y = f(x)$在点$P(1,f(1))$处的切线$l$过点$(2,0)$,且$f'(1)= - 2$,则$f(1)=$________.
答案:
2
9. 已知曲线$f(x)= - 3x^{2}+m$($m$为常数)在点$(1,f(1))$处的切线在$y$轴上的截距是$1$,则$m$的值是_________.
答案:
-2
10. 曲线$y=\sqrt{2x}(x\geqslant0)$在点$P(\frac{1}{2},1)$处的切线的斜率为_________.
答案:
1
11. 求曲线$y=(x + 1)^{2}$在点$P(1,4)$处的切线方程.
答案:
解:切线的斜率$k = \lim\limits_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=4$,
故切线方程为$y = 4x$。
故切线方程为$y = 4x$。
查看更多完整答案,请扫码查看


