《2025年53精准练九年级数学下册北师大版山西专版》

10. 如图，AB为⊙O的直径，BC是弦，将AC绕A点顺时针旋转得到AD，点D恰好落在⊙O上，AB交AD于E，若OE = EB，AB = 4，则BC的长是__________.

答案：
$\sqrt{2}$
详解：如图，连接CD交AB于点F，连接AC、AD、OC、OD、DE、BD.

∵将$\overset{\frown}{AC}$绕着A点顺时针旋转得到$\overset{\frown}{AD}$，
∴$\overset{\frown}{AC}=\overset{\frown}{AD}$，
∴AC = AD，
∴点A在CD的垂直平分线上，
∵OC = OD，
∴点O在CD的垂直平分线上，
∴AB垂直平分CD，
∴BC = BD，
∵∠BAD同时是$\overset{\frown}{BD}$，$\overset{\frown}{DE}$所对的圆周角，
∴$\overset{\frown}{BD}=\overset{\frown}{DE}$，
∴BD = DE，
∴EF = BF.
∵OE = EB，AB = 4，
∴OB = $\frac{1}{2}$AB = 2，
∴BE = $\frac{1}{2}$OB = 1，
∴BF = $\frac{1}{2}$BE = $\frac{1}{2}$.
∵AB为⊙O的直径，
∴∠ACB = 90° = ∠BFC，
∵∠ABC = ∠CBF，
∴△CBF∽△ABC，
∴$\frac{CB}{AB}=\frac{BF}{BC}$，即$\frac{CB}{4}=\frac{\frac{1}{2}}{BC}$，
∴BC = $\sqrt{2}$(负值舍去).

11. [2024晋中平遥县一模]如图，AB为⊙O的直径，点C，D都在⊙O上，CE//AB，若∠ADE = 25°，则∠ABC的度数为（ ）

A. 45°
B. 55°
C. 65°
D. 75°

答案： C

12. [2024忻州保德县三模改编]如图，点A、B、C、D在⊙O上，AC是⊙O的直径. 如果∠ACD = ∠DBC，CD = $\frac{5\sqrt{2}}{2}$，AB = 3，那么BC的长为（ ）

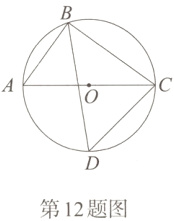
A. 3
B. $\frac{5}{2}$
C. 5
D. 4

答案： D

13. [2023朔州右玉县期中]如图，四边形ABCD是⊙O的内接四边形，BC是⊙O的直径，BC = 2CD，则∠BAD的度数是__________.

答案： 120°

14. 如图，点A、B、C、D都在⊙O上，若∠B与∠D互余，AB = 24，⊙O的半径为13，则CD的长度为__________.

答案：
10
详解：如图，连接AO并延长交⊙O于点E，连接BE，

∵AE是⊙O的直径，
∴∠ABE = 90°，
∴∠ABD + ∠EBD = 90°，AB² + BE² = AE².
∵∠ABD与∠D互余，
即∠ABD + ∠D = 90°，
∴∠D = ∠EBD，
∴$\overset{\frown}{BC}=\overset{\frown}{DE}$，
∴$\overset{\frown}{BE}=\overset{\frown}{CD}$，
∴BE = CD.
∵AB = 24，⊙O的半径为13，
∴24² + BE² = 26²，
∴BE = 10(负值舍去)，
∴CD = 10.

15. 如图，△ABC中，以AB为直径作⊙O，交BC于点D，交CA的延长线于点E，连接DE，DE = DC.
(1)求证：D是BC的中点；
(2)若∠C = 22.5°，AE = 2，求⊙O的半径.

答案：
解：
(1)证明：如图，连接AD.

∵DE = DC，
∴∠C = ∠AED，
又
∵∠AED = ∠ABD，
∴∠C = ∠ABD，
∴AB = AC，
∵AB为⊙O的直径，
∴AD⊥BC，
∴BD = CD，
即D是BC的中点.
(2)如图，连接BE，则∠AEB = 90°.

由
(1)知∠C = ∠ABD，
∴∠EAB = ∠C + ∠ABD = 2∠C = 45°，
∴AB = $\frac{AE}{\cos45^{\circ}}=\frac{2}{\frac{\sqrt{2}}{2}}$ = $2\sqrt{2}$，
∴OB = $\frac{1}{2}$AB = $\sqrt{2}$，
即⊙O的半径为$\sqrt{2}$.

16. [2024朔州一模]如图，△ABC的三个顶点均在⊙O上，BD是⊙O的直径. 若∠BAC = 130°，则∠CBD的度数为（ ）

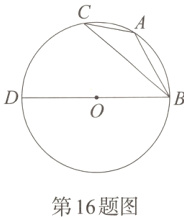
A. 30°
B. 40°
C. 45°
D. 50°

答案： B

17. 如图，点B、C、D都在⊙O上，E在BC的延长线上，若∠DCE = 55°，则∠BOD = __________.

答案： 110°