《2025年53精准练九年级数学下册北师大版山西专版》

1. 下列最有可能是函数$y = x^{2}$的图象的是（ ）

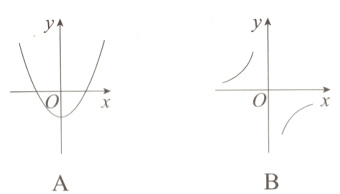
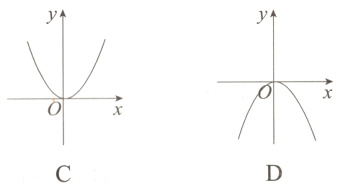
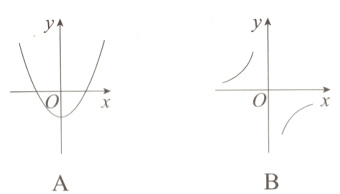
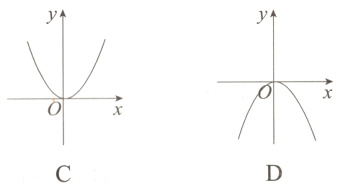
答案： C

2. 下列关于函数$y = x^{2}$的说法错误的是（ ）
A. 图象开口向上
B. $x ＞ 0$时，y随x的增大而减小
C. 图象关于y轴对称
D. 图象有最低点

答案： B

3. 已知点$(x_{1}, y_{1})$，$(x_{2}, y_{2})$都在抛物线$y = x^{2}$上，且$x_{1} ＜ x_{2} ＜ 0$，则$y_{1}$，$y_{2}$的大小关系是（ ）
A. $y_{1} ＜ y_{2}$
B. $y_{1} = y_{2}$
C. $y_{1} ＞ y_{2}$
D. 无法确定

答案： C

4. [原创题]下列关于点(0，0)与抛物线$y = x^{2}$的关系的说法：
①点(0，0)是抛物线$y = x^{2}$与x轴的交点；
②点(0，0)是抛物线$y = x^{2}$的顶点；
③点(0，0)是抛物线$y = x^{2}$的最高点；
④点(0，0)是抛物线$y = x^{2}$的最低点.
其中正确的是__________.(填序号)

答案： ①②④

5. 已知两点(a，5)，(b，5)都在抛物线$y = x^{2}$上，则$a + b$的值为__________.

答案： 0

6.[原创题]下列情境中的曲线可能看作抛物线$y = -x^{2}$的是 ( )

A. 亭顶边缘的轮廓
B. 古典园林的月洞门轮廓
C. 投出篮球的轨迹
D. 半圆尺的曲边

答案： C

7.下列关于函数$y = -x^{2}$的说法正确的是 ( )
A. 图象开口向上
B. y随x的增大而减小
C. 图象关于x轴对称
D. 无论x取何值，y的值总是非正数

答案： D

8.[原创题]已知点$(x_{1},y_{1}),(x_{2},y_{2})$都在抛物线$y = -x^{2}$上，且$y_{1}＜y_{2}＜0$，则下列大小关系正确的是 ( )
A. $x_{1}＜x_{2}$
B. $x_{1}＞x_{2}$
C. $x_{1}$与$x_{2}$的大小关系无法确定，但$|x_{1}|＜|x_{2}|$
D. $x_{1}$与$x_{2}$的大小关系无法确定，但$|x_{1}|＞|x_{2}|$

答案： D

9.二次函数$y = x^{2}$和$y = -x^{2}$共有的性质是 ( )
A. 图象开口向下
B. 图象关于y轴对称
C. 图象都有最低点
D. y随x的增大而减小

答案： B

10.若点$A(a,4)$关于x轴的对称点在抛物线$y = -x^{2}$上，则$a =$________.

答案： +2

1. 下列最有可能是函数$y = x^{2}$的图象的是（ ）
　　
　　
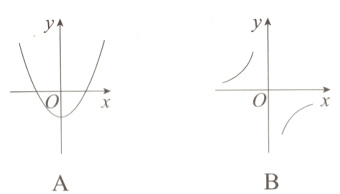
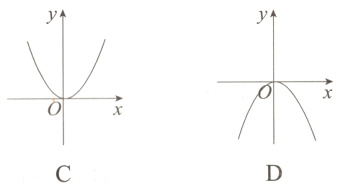
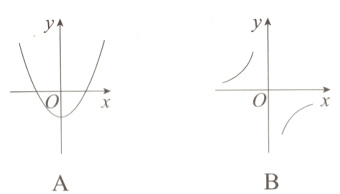
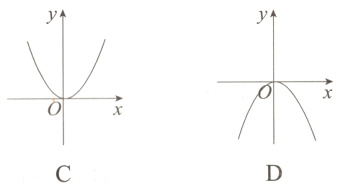
A.
B.
C.
D.

答案： C

2. 下列关于函数$y = x^{2}$的说法错误的是（ ）
A. 图象开口向上
B. $x ＞ 0$时，$y$随$x$的增大而减小
C. 图象关于$y$轴对称
D. 图象有最低点

答案： B

4. [原创题]下列关于点$(0,0)$与抛物线$y = x^{2}$的关系的说法：
①点$(0,0)$是抛物线$y = x^{2}$与$x$轴的交点；
②点$(0,0)$是抛物线$y = x^{2}$的顶点；
③点$(0,0)$是抛物线$y = x^{2}$的最高点；
④点$(0,0)$是抛物线$y = x^{2}$的最低点.
其中正确的是___________.(填序号)

答案： ①②④

5. 已知两点$(a,5)$，$(b,5)$都在抛物线$y = x^{2}$上，则$a + b$的值为___________.

答案： 0

6. [原创题]下列情境中的曲线可能看作抛物线$y = -x^{2}$的是（ ）
　　
A. 亭顶边缘的轮廓
B. 古典园林的月洞门轮廓
C. 投出篮球的轨迹
D. 半圆尺的曲边

答案： C

7. 下列关于函数$y = -x^{2}$的说法正确的是（ ）
A. 图象开口向上
B. $y$随$x$的增大而减小
C. 图象关于$x$轴对称
D. 无论$x$取何值，$y$的值总是非正数

答案： D

8. [原创题]已知点$(x_{1},y_{1})$，$(x_{2},y_{2})$都在抛物线$y = -x^{2}$上，且$y_{1} ＜ y_{2} ＜ 0$，则下列大小关系正确的是（ ）
A. $x_{1} ＜ x_{2}$
B. $x_{1} ＞ x_{2}$
C. $x_{1}$与$x_{2}$的大小关系无法确定，但$|x_{1}| ＜ |x_{2}|$
D. $x_{1}$与$x_{2}$的大小关系无法确定，但$|x_{1}| ＞ |x_{2}|$

答案： D

9. 二次函数$y = x^{2}$和$y = -x^{2}$共有的性质是（ ）
A. 图象开口向下
B. 图象关于$y$轴对称
C. 图象都有最低点
D. $y$随$x$的增大而减小

答案： B

10. 若点$A(a,4)$关于$x$轴的对称点在抛物线$y = -x^{2}$上，则$a =$________.

答案： ±2