2025年53精准练九年级数学下册北师大版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年53精准练九年级数学下册北师大版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
8. 在△ABC中,∠ABC = 30°,AB = $\sqrt{3}$,AC = 1,则∠ACB的度数为__________.
答案:
60°或120°
9. 如图,在△ABC中,AB = AC = 5,∠A = 120°,则BC的长是( )
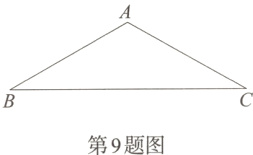
A. 8
B. 5$\sqrt{2}$
C. 5$\sqrt{3}$
D. $\frac{10\sqrt{3}}{3}$

A. 8
B. 5$\sqrt{2}$
C. 5$\sqrt{3}$
D. $\frac{10\sqrt{3}}{3}$
答案:
C
10. [2024朔州一模]如图是一面钟表,以指针的旋转中心O为坐标原点,以整9点时 时针和分针所在的直线分别为x轴和y轴建立如图所示的平面直角坐标系,当时间为10点10分时,分针的外端点落在点A处. 若OA = 10,则点A的坐标为( )

A. (5$\sqrt{3}$, 5)
B. (5, 5$\sqrt{3}$)
C. (5$\sqrt{2}$, 5$\sqrt{2}$)
D. (5$\sqrt{3}$, 5$\sqrt{2}$)

A. (5$\sqrt{3}$, 5)
B. (5, 5$\sqrt{3}$)
C. (5$\sqrt{2}$, 5$\sqrt{2}$)
D. (5$\sqrt{3}$, 5$\sqrt{2}$)
答案:
A
11. 如图,已知∠ACB = 90°,AC = 10,OB = 17,$\cos \angle OBC = \frac{3}{5}$,则点C的坐标为( )

A. (8, $\frac{27}{4}$)
B. (8, 12)
C. (6, $\frac{33}{4}$)
D. (6, 10)

A. (8, $\frac{27}{4}$)
B. (8, 12)
C. (6, $\frac{33}{4}$)
D. (6, 10)
答案:
B
详解: 如图所示, 过点C作CD⊥x轴于点D, CE⊥y轴于点E,
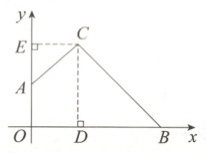
∵∠ACB = 90°, ∠AOB = 90°,
∴∠OBC + ∠OAC = 180°,
∵∠EAC + ∠OAC = 180°,
∴∠EAC = ∠OBC,
∵AC = 10, cos ∠OBC = 3/5,
∴cos ∠EAC = EA/AC = cos ∠OBC = 3/5,
∴EA = 6,
∴EC = √(AC² - EA²) = 8,
∴OD = EC = 8.
∵OB = 17,
∴BD = 9,
∵cos ∠OBC = BD/CB = 3/5,
∴CB = 15,
∴CD = √(CB² - DB²) = √(15² - 9²) = 12,
∴C(8, 12).
B
详解: 如图所示, 过点C作CD⊥x轴于点D, CE⊥y轴于点E,

∵∠ACB = 90°, ∠AOB = 90°,
∴∠OBC + ∠OAC = 180°,
∵∠EAC + ∠OAC = 180°,
∴∠EAC = ∠OBC,
∵AC = 10, cos ∠OBC = 3/5,
∴cos ∠EAC = EA/AC = cos ∠OBC = 3/5,
∴EA = 6,
∴EC = √(AC² - EA²) = 8,
∴OD = EC = 8.
∵OB = 17,
∴BD = 9,
∵cos ∠OBC = BD/CB = 3/5,
∴CB = 15,
∴CD = √(CB² - DB²) = √(15² - 9²) = 12,
∴C(8, 12).
12. 如图,在□ABCD中,∠AOB = 120°,BD = 20,则□ABCD的面积为__________.


答案:
50√3
13. [2024达州改编]如图,在Rt△ABC中,∠C = 90°. 点D在线段BC上,∠BAD = 45°. 若$\tan \angle ADC = 4$,CD = 1,求△ABC的面积.


答案:
解: 如图, 延长AD, 过点B向AD的延长线作垂线, 垂足记为E,
则有∠BDE = ∠ADC, tan ∠BDE = tan ∠ADC = 4.
在Rt△ACD中, tan ∠ADC = 4, CD = 1,
∴AC = CD·tan ∠ADC = 4,
∴AD = √(AC² + CD²) = √17.
在Rt△BED中, 设DE = x, 则BE = DE·tan ∠BDE = 4x,
∴BD = √(BE² + DE²) = √17x.
在Rt△BEA中, ∠BAD = 45°,
∴AE = BE = 4x,
又
∵AE = AD + DE = √17 + x,
∴4x = √17 + x,
解得x = √17/3,
∴BD = √17x = 17/3,
∴BC = BD + CD = 17/3 + 1 = 20/3,
∴S△ABC = 1/2 AC·BC = 40/3.
则有∠BDE = ∠ADC, tan ∠BDE = tan ∠ADC = 4.
在Rt△ACD中, tan ∠ADC = 4, CD = 1,
∴AC = CD·tan ∠ADC = 4,
∴AD = √(AC² + CD²) = √17.
在Rt△BED中, 设DE = x, 则BE = DE·tan ∠BDE = 4x,
∴BD = √(BE² + DE²) = √17x.
在Rt△BEA中, ∠BAD = 45°,
∴AE = BE = 4x,
又
∵AE = AD + DE = √17 + x,
∴4x = √17 + x,
解得x = √17/3,
∴BD = √17x = 17/3,
∴BC = BD + CD = 17/3 + 1 = 20/3,
∴S△ABC = 1/2 AC·BC = 40/3.
14. [推理能力·2024太原三模]如图,已知在Rt△ABC中,∠ACB = 90°,∠A = 30°,AB = 2,过点C作CD₁⊥AB于D₁,过点D₁作D₁D₂⊥AC于D₂,过点D₂作D₂D₃⊥AB于D₃,过点D₃作D₃D₄⊥AC于D₄,……,按此方法得到的D₇D₈的长为__________.


答案:
81/256详解: 根据∠ACB = 90°, ∠A = 30°, 得到∠B = 60°, BC = 1/2 AB = 1.
∵CD₁⊥AB,
∴∠BCD₁ = 30°,在△BCD₁中, ∠BD₁C = 90°, BC = 1, 则CD₁ = √3/2,进而在△CD₁D₂中,有D₁D₂ = √3/2 CD₁ = (√3/2)²,进而可得, D₂D₃ = (√3/2)³, ……则线段DₙDₙ₊₁ = (√3/2)ⁿ⁺¹.
∴D₇D₈ = (√3/2)⁸ = 81/256.
∵CD₁⊥AB,
∴∠BCD₁ = 30°,在△BCD₁中, ∠BD₁C = 90°, BC = 1, 则CD₁ = √3/2,进而在△CD₁D₂中,有D₁D₂ = √3/2 CD₁ = (√3/2)²,进而可得, D₂D₃ = (√3/2)³, ……则线段DₙDₙ₊₁ = (√3/2)ⁿ⁺¹.
∴D₇D₈ = (√3/2)⁸ = 81/256.
查看更多完整答案,请扫码查看


