《2025年53精准练九年级数学下册北师大版山西专版》

9. 如图，AB是⊙O的直径，点B是弧CD的中点，AB交弦CD于E，且CD = 2√3，BD = 2，则AB的长度为 （ ）

A. 2
B. 3
C. 4
D. 5

答案： C

10. 在⊙O中，弦AB和CD相交于点P，且AB⊥CD，如果AP = 4，PB = 4，CP = 2，那么⊙O的直径为 （ ）
A. 4
B. 5
C. 8
D. 10

答案： D

11. 一面墙上有一个矩形门洞，其宽为1.5米，高为2米，现将其改造成圆弧形门洞(如图)，则改造后圆弧形门洞的最高点离地面的高度是__________.

答案： 2.25米

12. [分类讨论]如图，一下水管道横截面为圆形，直径为260 cm，下雨前水面宽为100 cm，若雨后水面宽为240 cm，则水位上升__________cm.

答案： 70或170

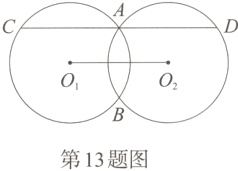
13. 如图，⊙O₁和⊙O₂相交于A和B两点，过点A作O₁O₂的平行线交两圆于点C、D，已知O₁O₂ = 20 cm，则CD = __________cm.

答案： 40

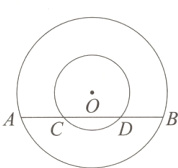
14. [教材P77习题3变式]如图，在两个同心圆中，大圆的弦AB与小圆相交于C，D两点.
(1)求证：AD = BC；
(2)若AC = 3，BC = 5，大圆的半径R = 5，求小圆的半径r的值.

答案： 解:
(1) 证明: 如图, 过O作OE⊥AB于点E, 由垂径定理可得AE = BE, CE = DE,
∴AE - CE = BE - DE,
∴AC = BD,
∴AD = BC.
(2) 如图, 连接OC, OA.
∵AC = 3, BC = 5,
∴AB = 3 + 5 = 8,
∴AE = 4,
∴CE = AE - AC = 4 - 3 = 1.
在Rt△AOE中, OE² = OA² - AE² = 5² - 4² = 9,
在Rt△COE中, OC² = CE² + OE² = 1² + 9 = 10,
∴OC = $\sqrt{10}$, 即小圆的半径r为$\sqrt{10}$.

15. [几何直观]如图，$AB$是直径，四边形$CDMN$和四边形$DEFG$都是正方形，其中点$C$、$D$、$E$在$AB$上，点$F$、$N$在半圆上. 若正方形$CDMN$的面积与正方形$DEFG$的面积之和是16，求$AB$的长.

答案： 解: 连接$ON$、$OF,$ 设正方形$CDMN$的边长为$a,$ 正方形$DEFG$的边长为$b,$ $OD$ $=$ $c,$ 则$CN$ $=$ $CD$ $=$ $a,$ $DE$ $=$ $EF$ $=$ $b,$
∵四边形$CDMN$和四边形$DEFG$都是正方形,
$∴∠NCD$ $=$ 90°, $∠FED$ $=$ 90°,
设$OA$ $=$ $ON$ $=$ $OF$ $=$ $OB$ $=$ $r,$
由勾股定理得$NC²$ $+$ $CO²$ $=$ $ON²,$ $EF²$ $+$ $OE²$ $=$ $OF²,$
即$a²$ $+$ $(a$ $+$ $c)²$ $=$ $r²①,$
$b²$ $+$ $(b$ - $c)²$ $=$ $r²②,$
① - ②, 得$a²$ $+$ $(a$ $+$ $c)²$ - $b²$ - $(b$ - $c)²$ $=$ 0, $(a²$ - $b²)$ $+$ $[(a$ $+$ $c)²$ - $(b$ - $c)²]$ $=$ 0,
$(a$ $+$ $b)(a$ - $b)$ $+$ $(a$ $+$ $c$ $+$ $b$ - $c)(a$ $+$ $c$ - $b$ $+$ $c)$ $=$ 0,
$(a$ $+$ $b)(a$ - $b)$ $+$ $(a$ $+$ $b)(a$ - $b$ $+$ $2c)$ $=$ 0,
$(a$ $+$ $b)(a$ - $b$ $+$ $a$ - $b$ $+$ $2c)$ $=$ 0,
$2(a$ $+$ $b)(a$ - $b$ $+$ $c)$ $=$ 0,
$∵a$ $+$ $b$ ≠ 0, $∴a$ - $b$ $+$ $c$ $=$ 0,
即$b$ $=$ $a$ $+$ $c.$
把$b$ $=$ $a$ $+$ $c$代入①, 得$a²$ $+$ $b²$ $=$ $r²,$
∵正方形$CDMN$的面积与正方形$DEFG$的面积之和是16,
$∴a²$ $+$ $b²$ $=$ 16,
$∴r²$ $=$ 16,
解得$r$ $=$ 4(负值舍去),
$∴AB$ $=$ $2r$ $=$ 8.