《2025年53精准练九年级数学下册北师大版山西专版》

11. [2023太原山大附中模拟改编]如图，抛物线$y = (x - 1)^2$与$x$轴只有一个公共点$M$，与平行于$x$轴的直线$l$交于点$A$、$B$，若$AB = 4$，则点$M$到直线$l$的距离为（ ）
　　
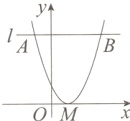
A. 2
B. 3
C. 4
D. 5

答案： C

12. 将抛物线$y = 2(x + 5)^2 + 3$绕其顶点旋转$180^{\circ}$就得到抛物线________________.

答案： $y = -2(x + 5)^2 + 3$

13. [跨学科·物理]某弹射装置从地面以6 m/s的速度竖直向上抛出一个物体，由物理知识可知，物体运动过程中离地面的高度$y$（单位：m）与运动时间$x$（单位：s）之间满足形如$y = -5(x - h)^2 + 5h^2$的函数关系. 经观测，物体运动1 s时，离地面的高度为1 m.
(1) 求$h$的值.
(2) 物体运动多长时间上升到最高位置？最高位置离地面的高度是多少？

答案： 解：
(1)由题意可知，抛物线$y = -5(x - h)^2 + 5h^2$经过点$(1,1)$，将$(1,1)$代入得$1 = -5(1 - h)^2 + 5h^2$，解得$h = 0.6$。
(2)$\because h = 0.6$，$\therefore y = -5(x - 0.6)^2 + 1.8$。当$x = 0.6$时，$y$取得最大值1.8。$\therefore$物体运动0.6 s上升到最高位置，最高位置离地面的高度是1.8 m。

14. [原创题]定义一种新运算“※”为$a※b = \begin{cases}a(b - a)^2, & b ＞ a, \\ -a(b - a)^2, & b\leq a.\end{cases}$下面探究函数$y = a※x$的图象和性质.
(1) 先从函数$y = 1※x$入手.
①$y = 1※x = \begin{cases}\_\_\_\_\_\_\_\_, & \_\_\_\_\_\_\_\_, \\ \_\_\_\_\_\_\_\_, & \_\_\_\_\_\_\_\_.\end{cases}$
②列表：
　　
画出函数$y = 1※x$的大致图象：
　　
③描述函数$y = 1※x$的图象的变化趋势和对称性.
(2) 直接描述函数$y = (-1)※x$的图象的变化趋势和对称性.
(3) 总结函数$y = a※x(a\neq0)$的图象的变化趋势和对称性.

答案：
解：
(1)①$(x - 1)^2$；$x ＞ 1$；$-(x - 1)^2$；$x\leq1$。
②如表所示。
x -1 0 1 2 3
y -4 -1 0 1 4
如图所示。


③$y$随$x$的增大而增大；函数图象关于点$(1,0)$中心对称。
(2)$y$随$x$的增大而减小；函数图象关于点$(-1,0)$中心对称。

(3)当$a ＞ 0$时，$y$随$x$的增大而增大，函数图象关于点$(a,0)$中心对称；当$a ＜ 0$时，$y$随$x$的增大而减小，函数图象关于点$(a,0)$中心对称。