《2025年53精准练九年级数学下册北师大版山西专版》

1.[2024大同平城区一模]cos 60°的值是 （ ）
A. $\frac{1}{2}$
B. 1
C. $\frac{\sqrt{3}}{2}$
D. $\sqrt{3}$

答案： A

2.在△ABC中，∠A = 105°，∠B = 30°，则tan C的值是 （ ）
A. $\frac{\sqrt{2}}{2}$
B. $\frac{\sqrt{3}}{3}$
C. 1
D. $\sqrt{3}$

答案： C

3.如图，以O为圆心，任意长为半径画弧，与射线OA交于点B，再以B为圆心，BO长为半径画弧，两弧交于点C，画射线OC，则sin (90° - ∠AOC)的值为 （ ）

A. $\frac{1}{2}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{\sqrt{3}}{2}$
D. $\frac{\sqrt{3}}{3}$

答案： A

4.已知实数a = tan 30°，b = cos 60°，c = sin 45°，则a，b，c的大小关系为________.(用“＞”连接)

答案： c ＞ a ＞ b

5. 计算
(1) 2sin 60° - tan 30°；
(2) sin 30° + 4cos 30°·tan 60° - cos²45°；
(3) 2cos 30° - tan 45° - $\sqrt{(1 - tan 60°)^2}$.

答案： 解:
(1)原式=2×$\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{3}=\frac{2\sqrt{3}}{3}$.
(2)原式=$\frac{1}{2}+4×\frac{\sqrt{3}}{2}×\sqrt{3}-(\frac{\sqrt{2}}{2})^{2}$
=$\frac{1}{2}+6-\frac{1}{2}$
=6.
(3)原式=2×$\frac{\sqrt{3}}{2}-1-\sqrt{(1 - \sqrt{3})^{2}}$
=$\sqrt{3}-1-\sqrt{3}+1$
=0.

6.在△ABC中，∠C = 90°，AB = $\sqrt{6}$，BC = $\sqrt{3}$，则∠A的度数为 （ ）
A. 30°
B. 45°
C. 60°
D. 75°

答案： B

7.若∠A是锐角，cos (A - 20°) = $\frac{1}{2}$，则∠A的度数为________.

答案： 80°

8.已知锐角A满足关系式4sin²A - 8sin A + 3 = 0，则∠A的度数为________.

答案： 30°

9.[跨学科·物理]桔槔俗称“吊杆”“称杆”(如图1)，是我国古代农用工具，始见于《墨子·备城门》，是一种利用杠杆原理的取水机械. 桔槔示意图如图2所示，OM是垂直于水平地面的支撑杆，OM = 3米，AB是杠杆，AB = 6米，OA:OB = 2:1. 当点A位于最高点时，∠AOM = 120°. 此时A到地面的距离为 （ ）


A. (2$\sqrt{3}$ + 3)米
B. 5米
C. 6米
D. 7米

答案： B

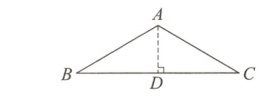
10.[2023长治期末]在2023中国国际大数据产业博览会上，某自动化立体库中有许多几何元素，其中有一个等腰三角形模型，如图，tan B = $\frac{\sqrt{3}}{3}$，AB = AC = 12 m，求△ABC的面积.

答案：
解:如图,作AD⊥BC,垂足为D.

∵tan B=$\frac{\sqrt{3}}{3}$,
∴∠B = 30°,
∵AB = AC = 12 m,AD⊥BC,
∴AD=$\frac{1}{2}$AB = 6 m,BC = 2BD,
在Rt△ABD中,BD=$\sqrt{AB^{2}-AD^{2}}=\sqrt{12^{2}-6^{2}} = 6\sqrt{3}$(m),
∴BC = 2BD = 12$\sqrt{3}$m,
∴$S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}×12\sqrt{3}×6 = 36\sqrt{3}$($m^{2}$).