《2025年53精准练九年级数学下册北师大版山西专版》

11. [2024赤峰]如图，AD是⊙O的直径，AB是⊙O的弦，半径OC⊥AB，连接CD，交OB于点E，∠BOC = 42°，则∠OED的度数是 （ ）

A. 61°
B. 63°
C. 65°
D. 67°

答案： B

12. [2023吕梁联考改编]如图，已知AB是⊙O的直径，弦CD⊥AB，垂足为E，∠ACD = 67.5°，AB = 4，则CD的长为 （ ）

A. $\sqrt{2}$
B. 2
C. $2\sqrt{2}$
D. $4\sqrt{2}$

答案： C

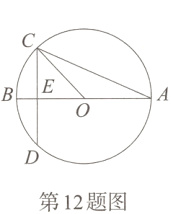
13. [2024长治壶关县多校联考期末]如图，四边形ABCD的顶点都在⊙O上，AB = AC = 10，BC = $4\sqrt{5}$，AC⊥BD，垂足为E，则DE的长为__________.

答案： 3
详解:如图,作AF⊥BC于F.
∵AB = AC = 10, BC = 4√5,
∴BF = 1/2BC = 2√5,
由勾股定理得，
AF = √(AB² - BF²) = 4√5
S△ABC = 1/2BC·AF = 1/2AC·BE,
即1/2×4√5×4√5 = 1/2×10×BE,
解得BE = 8.
由勾股定理得，
AE = √(AB² - BE²) = 6,
∴CE = AC - AE = 4.
∵⌢AD = ⌢AD,
∴∠DCE = ∠ABE,
又
∵∠DEC = 90° = ∠AEB,
∴△DCE∽△ABE,
∴DE/AE = CE/BE, 即DE/6 = 4/8,
解得DE = 3.

14. 如图，已知在⊙O中，AB，CD为直径，弦DE⊥AB于点F，连接BC，BE. 若DC//BE，求∠C的度数.

答案： 解:
∵DC//BE,
∴∠C = ∠CBE,
∵∠CBE = ∠CDE,
∴∠C = ∠CDE.
∵OB = OC,
∴∠OBC = ∠C,
∴∠DOB = ∠OBC + ∠C = 2∠C.
在△OFD中, ∠OFD = 90°, ∠CDE = ∠C, ∠DOF = 2∠C,
可得90° + ∠C + 2∠C = 180°,
解得∠C = 30°.

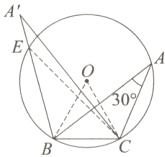
15. [探究情境]在“圆周角”一课的探究活动中，李老师设计了一份活动单：

学习小组通过操作、观察、讨论后得到：点$A$的位置不唯一，它在以$BC$为弦的圆弧上(点$B$、$C$除外) ……小华同学画出了符合要求的一条圆弧(如图)，即圆中的优弧$BAC.$
【展示交流】
(1)在展示交流中经过比对发现，小明同学所画的角的顶点不在小华所画的圆弧上，而在如图所示的弓形外部，我们记为$A'$，请你利用下图证明$∠BA'C$ ＜ 30°.

【提出问题】
(2)展示交流后，小华同学提出了下列新问题，请你帮助解决.
①求该弧所在圆$O$的半径；
$②△ABC$面积的最大值为__________.

答案：
解:
(1)证明:如图，设$A'B$交$⊙O$于$E,$连接$CE.$
由圆周角定理的推论可知
$∠BEC$ $=$ $∠BAC$ $=$ 30°,
$∵∠BEC$是$△A'EC$的外角，
$∴∠BA'C$ ＜ $∠BEC,$
即$∠BA'C$ ＜ 30°.

$(2)①$如图,连接$BO$、$CO.$
$∵∠BAC$ $=$ 30°,
$∴∠BOC$ $=$ 60°,
$∵OB$ $=$ $OC,$
$∴△OBC$是等边三角形,
$∴OB$ $=$ $OC$ $=$ $BC$ $=$ 4,即半径为4.
②8 $+$ 4√3.
详解$:△ABC$以$BC$为底边,当点$A$到$BC$ 的距离最大时$,△ABC$的面积最大.
如图,过点$O$作$BC$的垂线,垂足为$E,$延长$EO,$交圆于$D,$则当$A$与$D$重合时$,△ABC$的面积最大,

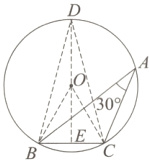
$∴BE$ $=$ $CE$ $=$ 2, $DO$ $=$ $BO$ $=$ 4,
$∴OE$ $=$ $√(BO²$ - $BE²)$ $=$ 2√3,
$∴DE$ $=$ $DO$ $+$ $OE$ $=$ 4 $+$ 2√3,
$∴△ABC$的最大面积为$1/2×4×(4$ $+$ $2√3)$ $=$ 8 $+$ 4√3.