《2025年53精准练九年级数学下册北师大版山西专版》

9. 已知抛物线$y=x^{2}+(3m - 1)x - 3m(m\gt0)$的最低点的纵坐标为$-4$，则抛物线的表达式是 （ ）
A. $y=x^{2}-6x+5$
B. $y=x^{2}+2x-3$
C. $y=x^{2}+5x-6$
D. $y=x^{2}+4x-5$

答案： B

10. 二次函数$y=ax^{2}+2ax+b(a\neq0$且$a\gt b)$中，当$-1\leq x\leq4$时，$-2\leq y\leq3$，则$a=$________，$b=$________.

答案： $0.2$；$-1.8$

11. [新定义]在平面直角坐标系中，如果点$P$的横坐标与纵坐标相等，则称点$P$为和谐点，例如：点$(1,1)$、$(-2,-2)$、$(0.5,0.5)$都是和谐点. 若二次函数$y=ax^{2}+7x+c(a\neq0)$的图象上有且只有一个和谐点$(-1,-1)$，则此二次函数的表达式为________________.

答案： $y = 3x^{2}+7x + 3$

12. [2023南京外国语学校月考]如图，抛物线经过$A(-3,0)$，$B(0,6)$两点，且其对称轴为直线$x=-1$.
(1)求此抛物线及直线$AB$的函数表达式；
(2)$P$是抛物线上点$A$与点$B$之间的动点(不包括点$A$，点$B$)，若$\triangle PAB$的面积为6，求此时点$P$的坐标.

答案： 解：
(1)$\because$抛物线经过$A(-3,0)$，且其对称轴为直线$x = -1$，
$\therefore$抛物线与$x$轴的另一交点坐标为$(1,0)$。
设抛物线的表达式为$y = a(x + 3)(x - 1)(a\neq 0)$，
把$B(0,6)$代入上式得$-3a = 6$，
解得$a = -2$，
$\therefore$抛物线的表达式为$y=-2(x + 3)\cdot(x - 1)$，即$y=-2x^{2}-4x + 6$。
设直线$AB$的表达式为$y_{AB}=kx + b$
$(k\neq 0)$，根据题意得$\begin{cases}-3k + b = 0,\\b = 6,\end{cases}$
解得$\begin{cases}k = 2,\\b = 6,\end{cases}$
$\therefore y_{AB}=2x + 6$。
(2)设$P(m,-2m^{2}-4m + 6)$，其中$-3 ＜ m ＜ 0$，
过点$P$作$PC\perp x$轴交$AB$于点$C$，
则$C(m,2m + 6)$，$\therefore PC=-2m^{2}-4m + 6 - 2m - 6=-2m^{2}-6m$，
根据题意得$S_{\triangle PAB}=\dfrac{1}{2}(-2m^{2}-6m)\cdot3 = 6$，解得$m_{1}=-1$，$m_{2}=-2$，
$\therefore$点$P$的坐标为$(-1,8)$或$(-2,6)$。

13. [跨学科·物理·原创题]
【问题情境】小明周末外出骑行，自行车匀速驶过自行车道入口之后开始均匀加速.
【实验观察】
(1)下表是小明记录的自行车在自行车道上行驶的路程$y$(米)与时间$x$(秒)的数据：
|时间$x$/秒|0|1|2|3|4|
|----|----|----|----|----|----|
|路程$y$/米|0|1.25|3|5.25|8|
请你利用数据画出图象.

【探索发现】
(2)由物理知识可知，$y$是$x$的二次函数. 请根据表中数据及图象，确定$y$与$x$之间的函数表达式.
【结论应用】
(3)小明能稳定维持的最大骑行速度是5米/秒，他均匀加速骑行24米刚好达到这一速度，那么小明加速用了多长时间？

答案：
解：
(1)如图所示。

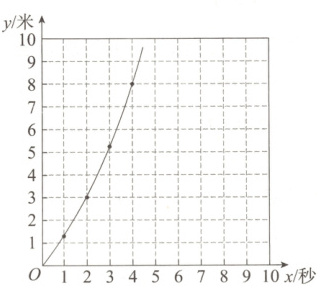
(2)由
(1)知抛物线经过原点，设其表达式为$y = ax^{2}+bx$，将$(2,3)$和$(4,8)$两点坐标代入得，
$\begin{cases}3 = 4a + 2b,\\8 = 16a + 4b,\end{cases}$
解得$\begin{cases}a = 0.25,\\b = 1.\end{cases}$
所以函数表达式为$y = 0.25x^{2}+x$。
(3)令$y = 24$，则$24 = 0.25x^{2}+x$，
解得$x_{1}=8$，$x_{2}=-12$(不合题意，舍去)。
所以小明加速用了8秒。