《2025年师说高中数学选择性必修第一册》

【问题探究1】把椭圆定义中的“距离之和”改为“距离之差的绝对值等于常数(小于$\vert F_{1}F_{2}\vert$)”，那么点的轨迹会怎么样？

答案：
问题探究1 提示：准备实验（可以找三名同学在教师指导下操作），适当选取两定点$F_1$，$F_2$，将拉锁拉开一段，其中一边的端点固定在$F_1$处，在另一边上截取一段（小于$|F_1F_2|$），作为动点$P$到两定点$F_1$和$F_2$距离之差，而后把它固定在$F_2$处，这时将铅笔（粉笔）置于$P$处，于是随着拉链逐渐打开，铅笔就画出一条曲线，同理可画出另一支.（如图）显然所画的曲线不是椭圆，而是两条相同的曲线，只是位置不同，其原因都是应用了“到两定点的距离之差$|PF_1|-|PF_2|$或$|PF_2|-|PF_1|$是同一个常数”这个条件

例1 已知点$F_{1}(-5,0)$，$F_{2}(5,0)$，动点$P$满足$\vert PF_{1}\vert - \vert PF_{2}\vert = 2a$，当$a$为3和5时，点$P$的轨迹分别是 （ ）
A.双曲线的右支
B.双曲线和一条射线
C.双曲线的一支和一条直线
D.双曲线的一支和一条射线

答案： 解析:依题意得$\vert F_{1}F_{2}\vert = 10$，
当$a = 3$时，$2a = 6 ＜ \vert F_{1}F_{2}\vert$，且$\vert PF_{1}\vert - \vert PF_{2}\vert = 6 ＞ 0$，点$P$的轨迹为双曲线的右支；
当$a = 5$时，$2a = 10 = \vert F_{1}F_{2}\vert$，故点$P$的轨迹为一条射线.故选D.
答案:D

巩固练习1 在平面直角坐标系$xOy$中，已知点$F_{1}(-5,0)$，$F_{2}(5,0)$，动点$P$满足$\vert PF_{2}\vert - \vert PF_{1}\vert = 8$，则动点$P$的轨迹是 （ ）
A.一条射线
B.双曲线的左支
C.双曲线的右支
D.双曲线的两支

答案： 解析:因为$F_{1}(-5,0)$，$F_{2}(5,0)$，所以$\vert F_{1}F_{2}\vert = 10$，若动点$P$满足$\vert\vert PF_{1}\vert - \vert PF_{2}\vert\vert = 8 ＜ \vert F_{1}F_{2}\vert = 10$，则动点$P$的轨迹是以$F_{1}$，$F_{2}$为焦点的双曲线.
而题目中动点$P$只满足$\vert PF_{2}\vert - \vert PF_{1}\vert = 8$，有$\vert PF_{2}\vert ＞ \vert PF_{1}\vert$，所以动点$P$的轨迹是以$F_{1}$，$F_{2}$为焦点的双曲线的左支.故选B.
答案:B

【问题探究2】类比求椭圆标准方程的过程.如何建立适当的坐标系，求出双曲线的标准方程？

答案：
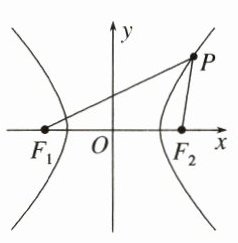
问题探究2 提示：观察我们画出的双曲线，发现它也具有对称性，而且直线$F_1F_2$是它的一条对称轴，所以以$F_1$，$F_2$所在直线为$x$轴，线段$F_1F_2$的垂直平分线为$y$轴，建立平面直角坐标系$Oxy$， 此时双曲线的焦点分别为$F_1(-c,0)$，$F_2(c,0)$，焦距为$2c$，$c > 0$. 设$P(x,y)$是双曲线上一点，则$||PF_1|-|PF_2|| = 2a$（$a$为大于0的常数）， 因为$|PF_1| = \sqrt{(x + c)^2 + y^2}$，$|PF_2| = \sqrt{(x - c)^2 + y^2}$， 所以$\sqrt{(x + c)^2 + y^2}-\sqrt{(x - c)^2 + y^2} = \pm 2a$，① 类比椭圆标准方程的化简过程，化简①，得$(c^2 - a^2)x^2 - a^2y^2 = a^2(c^2 - a^2)$，两边同除以$a^2(c^2 - a^2)$，得$\frac{x^2}{a^2}-\frac{y^2}{c^2 - a^2} = 1$. 由双曲线的定义知，$2c > 2a$，即$c > a$，所以$c^2 - a^2 > 0$，类比椭圆标准方程的建立过程，令$b^2 = c^2 - a^2$，其中$b > 0$，代入上式，得$\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1$（$a > 0$，$b > 0$）. 类似的方法，将焦点置于$y$轴时，可得焦点在$y$轴的双曲线的标准方程：$\frac{y^2}{a^2}-\frac{x^2}{b^2} = 1$（$a > 0$，$b > 0$）

例2 求满足下列条件的双曲线的标准方程.
(1)经过点$A(4\sqrt{2},3)$，且$a = 4$；
(2)经过点$A(2,\frac{2\sqrt{3}}{3})$，$B(3,-2\sqrt{2})$.

答案： 解析:
(1)因为$a = 4 ＞ 3$，可知双曲线的焦点在$x$轴上，设双曲线的标准方程为$\frac{x^{2}}{16}-\frac{y^{2}}{b^{2}} = 1$，
代入$A(4\sqrt{2},3)$，即$\frac{32}{16}-\frac{9}{b^{2}} = 1$，解得$b^{2} = 9$，
所以双曲线的标准方程为$\frac{x^{2}}{16}-\frac{y^{2}}{9} = 1$.
(2)方法一　若焦点在$x$轴上，则设双曲线的方程为$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} = 1$（$a ＞ 0$，$b ＞ 0$），
由于点$A(2,\frac{2\sqrt{3}}{3})$，$B(3,-2\sqrt{2})$在双曲线上，
所以$\begin{cases}\frac{4}{a^{2}}-\frac{\frac{4}{3}}{b^{2}} = 1\\\frac{9}{a^{2}}-\frac{8}{b^{2}} = 1\end{cases}$，解得$\begin{cases}a^{2} = 3\\b^{2} = 4\end{cases}$，
所以双曲线的标准方程为$\frac{x^{2}}{3}-\frac{y^{2}}{4} = 1$.
若焦点在$y$轴上，则设双曲线的方程为$\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}} = 1$（$a ＞ 0$，$b ＞ 0$），则$\begin{cases}\frac{\frac{4}{3}}{a^{2}}-\frac{4}{b^{2}} = 1\\\frac{8}{a^{2}}-\frac{9}{b^{2}} = 1\end{cases}$，解得$a^{2} = - 4$，$b^{2} = - 3$（舍去）.
方法二　设双曲线的标准方程为$mx^{2} - ny^{2} = 1$（$mn ＞ 0$），
代入点$A(2,\frac{2\sqrt{3}}{3})$，$B(3,-2\sqrt{2})$可得$\begin{cases}4m-\frac{4}{3}n = 1\\9m - 8n = 1\end{cases}$，解得$\begin{cases}m=\frac{1}{3}\\n=\frac{1}{4}\end{cases}$，所以双曲线的标准方程为$\frac{x^{2}}{3}-\frac{y^{2}}{4} = 1$.

巩固练习2 (1)若方程$\frac{x^{2}}{1 - m}+\frac{y^{2}}{m}=1$表示双曲线，则实数$m$的取值范围为 （ ）
A.$0 ＜ m ＜ 1$
B.$m ＜ 0$或$m ＞ 1$
C.$m ＜ 0$
D.$m ＞ 1$

答案： 解析:因为方程$\frac{x^{2}}{1 - m}+\frac{y^{2}}{m} = 1$表示双曲线，所以$(1 - m)m ＜ 0$，解得$m ＜ 0$或$m ＞ 1$. 故选B.

巩固练习2 (2)经过点$(\frac{4\sqrt{3}}{3},2\sqrt{3})$且焦点为$(0,-5)$，$(0,5)$的双曲线的标准方程是_______.

答案： 双曲线的焦点在$y$轴上，且$c = 5$，
因为双曲线过点$(\frac{4\sqrt{3}}{3},2\sqrt{3})$，根据双曲线的定义得：$2a=\left|\sqrt{(\frac{4\sqrt{3}}{3})^{2}+(2\sqrt{3}+5)^{2}}-\sqrt{(\frac{4\sqrt{3}}{3})^{2}+(2\sqrt{3}-5)^{2}}\right| = 6$，
则$a = 3$，则$b^{2} = c^{2} - a^{2} = 16$，
所以双曲线的标准方程为$\frac{y^{2}}{9}-\frac{x^{2}}{16} = 1$.
答案:
(2)$\frac{y^{2}}{9}-\frac{x^{2}}{16} = 1$