2025年师说高中数学选择性必修第一册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年师说高中数学选择性必修第一册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
题型二 由椭圆的几何性质求标准方程
例2 求适合下列条件的椭圆的标准方程.
(1)焦点在x轴上,a = 6,e = $\frac{1}{3}$;
(2)长轴长等于20,离心率等于$\frac{3}{5}$.
例2 求适合下列条件的椭圆的标准方程.
(1)焦点在x轴上,a = 6,e = $\frac{1}{3}$;
(2)长轴长等于20,离心率等于$\frac{3}{5}$.
答案:
例2 解析:
(1)因为椭圆的焦点在$x$轴上,设所求椭圆的标准方程为$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$,
令$c=\sqrt{a^{2}-b^{2}}$,则$e=\frac{c}{a}=\frac{c}{6}=\frac{1}{3}$,则$c = 2$,所以$b^{2}=a^{2}-c^{2}=36 - 4=32$,
因此所求椭圆的标准方程为$\frac{x^{2}}{36}+\frac{y^{2}}{32}=1$.
(2)设椭圆的长轴长、短轴长、焦距分别为$2a$,$2b$,$2c$,
由题意可得$2a = 20$,则$a = 10$,$\frac{c}{a}=\frac{c}{10}=\frac{3}{5}$,则$c = 6$,所以$b=\sqrt{a^{2}-c^{2}}=\sqrt{10^{2}-6^{2}}=8$,
当椭圆的焦点在$x$轴上时,则椭圆的标准方程为$\frac{x^{2}}{100}+\frac{y^{2}}{64}=1$;当椭圆的焦点在$y$轴上时,则椭圆的标准方程为$\frac{y^{2}}{100}+\frac{x^{2}}{64}=1$.
(1)因为椭圆的焦点在$x$轴上,设所求椭圆的标准方程为$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$,
令$c=\sqrt{a^{2}-b^{2}}$,则$e=\frac{c}{a}=\frac{c}{6}=\frac{1}{3}$,则$c = 2$,所以$b^{2}=a^{2}-c^{2}=36 - 4=32$,
因此所求椭圆的标准方程为$\frac{x^{2}}{36}+\frac{y^{2}}{32}=1$.
(2)设椭圆的长轴长、短轴长、焦距分别为$2a$,$2b$,$2c$,
由题意可得$2a = 20$,则$a = 10$,$\frac{c}{a}=\frac{c}{10}=\frac{3}{5}$,则$c = 6$,所以$b=\sqrt{a^{2}-c^{2}}=\sqrt{10^{2}-6^{2}}=8$,
当椭圆的焦点在$x$轴上时,则椭圆的标准方程为$\frac{x^{2}}{100}+\frac{y^{2}}{64}=1$;当椭圆的焦点在$y$轴上时,则椭圆的标准方程为$\frac{y^{2}}{100}+\frac{x^{2}}{64}=1$.
巩固练习2 (1)若椭圆的对称轴为坐标轴,长轴长与短轴长的和为18,一个焦点的坐标是(3,0),则椭圆的标准方程为______.
(2)已知椭圆的对称轴是坐标轴,O为坐标原点,F是一个焦点,A是一个顶点,椭圆的长轴长为6,且cos∠OFA = $\frac{2}{3}$,则椭圆的标准方程是______.
答案:
巩固练习2 解析:
(1)由题意,得$\begin{cases}2a + 2b = 18\\c = 3\\a^{2}=b^{2}+c^{2}\end{cases}$,
解得$\begin{cases}a = 5\\b = 4\end{cases}$.
因为椭圆的焦点在$x$轴上,
所以椭圆的标准方程为$\frac{x^{2}}{25}+\frac{y^{2}}{16}=1$.
(2)因为椭圆的长轴长是6,$\cos\angle OFA=\frac{2}{3}$,所以点$A$不是长轴的端点(是短轴的端点).
所以$|OF| = c$,$|AF| = a = 3$,
所以$\frac{c}{3}=\frac{2}{3}$,所以$c = 2$,$b^{2}=3^{2}-2^{2}=5$,
所以椭圆的标准方程是$\frac{x^{2}}{9}+\frac{y^{2}}{5}=1$或$\frac{x^{2}}{5}+\frac{y^{2}}{9}=1$.
答案:
(1)$\frac{x^{2}}{25}+\frac{y^{2}}{16}=1$
(2)$\frac{x^{2}}{9}+\frac{y^{2}}{5}=1$或$\frac{x^{2}}{5}+\frac{y^{2}}{9}=1$
(1)由题意,得$\begin{cases}2a + 2b = 18\\c = 3\\a^{2}=b^{2}+c^{2}\end{cases}$,
解得$\begin{cases}a = 5\\b = 4\end{cases}$.
因为椭圆的焦点在$x$轴上,
所以椭圆的标准方程为$\frac{x^{2}}{25}+\frac{y^{2}}{16}=1$.
(2)因为椭圆的长轴长是6,$\cos\angle OFA=\frac{2}{3}$,所以点$A$不是长轴的端点(是短轴的端点).
所以$|OF| = c$,$|AF| = a = 3$,
所以$\frac{c}{3}=\frac{2}{3}$,所以$c = 2$,$b^{2}=3^{2}-2^{2}=5$,
所以椭圆的标准方程是$\frac{x^{2}}{9}+\frac{y^{2}}{5}=1$或$\frac{x^{2}}{5}+\frac{y^{2}}{9}=1$.
答案:
(1)$\frac{x^{2}}{25}+\frac{y^{2}}{16}=1$
(2)$\frac{x^{2}}{9}+\frac{y^{2}}{5}=1$或$\frac{x^{2}}{5}+\frac{y^{2}}{9}=1$
题型三 求椭圆的离心率
【问题探究2】观察图,我们发现,不同椭圆的扁平程度不同,扁平程度是椭圆的重要形状特征,你能用适当的量定量刻画椭圆的扁平程度吗?这个定量对椭圆的形状有何影响?
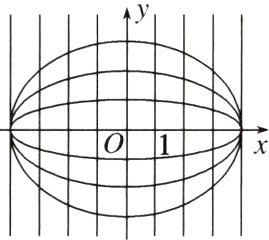
【问题探究2】观察图,我们发现,不同椭圆的扁平程度不同,扁平程度是椭圆的重要形状特征,你能用适当的量定量刻画椭圆的扁平程度吗?这个定量对椭圆的形状有何影响?

答案:
问题探究2 提示:利用离心率$e=\frac{c}{a}$来刻画椭圆的扁平程度.如图所示,在$Rt\triangle BF_2O$中,
$\cos\angle BF_2O=\frac{c}{a}$,记$e=\frac{c}{a}$,
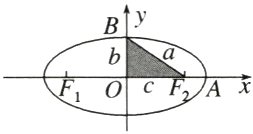
则$0<e<1$,$e$越大,$\angle BF_2O$越小,椭圆越扁;$e$越小,$\angle BF_2O$越大,椭圆越接近于圆.
问题探究2 提示:利用离心率$e=\frac{c}{a}$来刻画椭圆的扁平程度.如图所示,在$Rt\triangle BF_2O$中,
$\cos\angle BF_2O=\frac{c}{a}$,记$e=\frac{c}{a}$,

则$0<e<1$,$e$越大,$\angle BF_2O$越小,椭圆越扁;$e$越小,$\angle BF_2O$越大,椭圆越接近于圆.
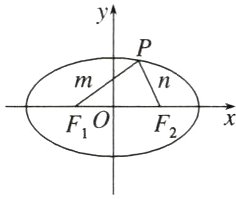
例3 设椭圆C:$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$的左、右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2 = 30°,求C的离心率.
变式练1 若将本例中“PF2⊥F1F2,∠PF1F2 = 30°”改为“∠PF2F1 = 75°,∠PF1F2 = 45°”,求C的离心率.
变式练2 若将本例中“PF2⊥F1F2,∠PF1F2 = 30°”改为“C上存在点P,使∠F1PF2为钝角”,求C的离心率的取值范围.
变式练1 若将本例中“PF2⊥F1F2,∠PF1F2 = 30°”改为“∠PF2F1 = 75°,∠PF1F2 = 45°”,求C的离心率.
变式练2 若将本例中“PF2⊥F1F2,∠PF1F2 = 30°”改为“C上存在点P,使∠F1PF2为钝角”,求C的离心率的取值范围.
答案:
例3 解析:方法一 由题意可设$|PF_2| = m$,结合条件可知$|PF_1| = 2m$,$|F_1F_2|=\sqrt{3}m$,故离心率$e=\frac{c}{a}=\frac{2c}{2a}=\frac{|F_1F_2|}{|PF_1|+|PF_2|}=\frac{\sqrt{3}m}{2m + m}=\frac{\sqrt{3}}{3}$.
方法二 由$PF_2\perp F_1F_2$可知$P$点的横坐标为$c$,将$x = c$代入椭圆方程可解得$y=\pm\frac{b^{2}}{a}$,所以$|PF_2|=\frac{b^{2}}{a}$. 又由$\angle PF_1F_2 = 30^{\circ}$可得$|F_1F_2|=\sqrt{3}|PF_2|$,故$2c=\sqrt{3}\cdot\frac{b^{2}}{a}$,变形可得$\sqrt{3}(a^{2}-c^{2})=2ac$,等式两边同除以$a^{2}$,得$\sqrt{3}(1 - e^{2})=2e$,解得$e=\frac{\sqrt{3}}{3}$或$e=-\sqrt{3}$(舍去).
变式练1 解析:在$\triangle PF_1F_2$中,
$\because\angle PF_1F_2 = 45^{\circ}$,$\angle PF_2F_1 = 75^{\circ}$,
$\therefore\angle F_1PF_2 = 60^{\circ}$,
设$|PF_1| = m$,$|PF_2| = n$,$|F_1F_2| = 2c$,$m + n = 2a$,
则在$\triangle PF_1F_2$中,有$\frac{m}{\sin75^{\circ}}=\frac{n}{\sin45^{\circ}}=\frac{2c}{\sin60^{\circ}}$,
$\therefore\frac{m + n}{\sin75^{\circ}+\sin45^{\circ}}=\frac{2c}{\sin60^{\circ}}$,
$\therefore e=\frac{c}{a}=\frac{2c}{2a}=\frac{\sin60^{\circ}}{\sin75^{\circ}+\sin45^{\circ}}=\frac{\sqrt{6}-\sqrt{2}}{2}$.
变式练2 解析:由题意,知$c>b$,$\therefore c^{2}>b^{2}$.
又$b^{2}=a^{2}-c^{2}$,
$\therefore c^{2}>a^{2}-c^{2}$,即$2c^{2}>a^{2}$.$\therefore e^{2}=\frac{c^{2}}{a^{2}}>\frac{1}{2}$,
$\therefore e>\frac{\sqrt{2}}{2}$,又$0<e<1$,
$\therefore C$的离心率的取值范围为$(\frac{\sqrt{2}}{2},1)$.
例3 解析:方法一 由题意可设$|PF_2| = m$,结合条件可知$|PF_1| = 2m$,$|F_1F_2|=\sqrt{3}m$,故离心率$e=\frac{c}{a}=\frac{2c}{2a}=\frac{|F_1F_2|}{|PF_1|+|PF_2|}=\frac{\sqrt{3}m}{2m + m}=\frac{\sqrt{3}}{3}$.
方法二 由$PF_2\perp F_1F_2$可知$P$点的横坐标为$c$,将$x = c$代入椭圆方程可解得$y=\pm\frac{b^{2}}{a}$,所以$|PF_2|=\frac{b^{2}}{a}$. 又由$\angle PF_1F_2 = 30^{\circ}$可得$|F_1F_2|=\sqrt{3}|PF_2|$,故$2c=\sqrt{3}\cdot\frac{b^{2}}{a}$,变形可得$\sqrt{3}(a^{2}-c^{2})=2ac$,等式两边同除以$a^{2}$,得$\sqrt{3}(1 - e^{2})=2e$,解得$e=\frac{\sqrt{3}}{3}$或$e=-\sqrt{3}$(舍去).
变式练1 解析:在$\triangle PF_1F_2$中,
$\because\angle PF_1F_2 = 45^{\circ}$,$\angle PF_2F_1 = 75^{\circ}$,
$\therefore\angle F_1PF_2 = 60^{\circ}$,
设$|PF_1| = m$,$|PF_2| = n$,$|F_1F_2| = 2c$,$m + n = 2a$,
则在$\triangle PF_1F_2$中,有$\frac{m}{\sin75^{\circ}}=\frac{n}{\sin45^{\circ}}=\frac{2c}{\sin60^{\circ}}$,
$\therefore\frac{m + n}{\sin75^{\circ}+\sin45^{\circ}}=\frac{2c}{\sin60^{\circ}}$,
$\therefore e=\frac{c}{a}=\frac{2c}{2a}=\frac{\sin60^{\circ}}{\sin75^{\circ}+\sin45^{\circ}}=\frac{\sqrt{6}-\sqrt{2}}{2}$.

变式练2 解析:由题意,知$c>b$,$\therefore c^{2}>b^{2}$.
又$b^{2}=a^{2}-c^{2}$,
$\therefore c^{2}>a^{2}-c^{2}$,即$2c^{2}>a^{2}$.$\therefore e^{2}=\frac{c^{2}}{a^{2}}>\frac{1}{2}$,
$\therefore e>\frac{\sqrt{2}}{2}$,又$0<e<1$,
$\therefore C$的离心率的取值范围为$(\frac{\sqrt{2}}{2},1)$.
巩固练习3 (1)已知椭圆C:$\frac{x^{2}}{a}+\frac{y^{2}}{b}=1(a>0,b>0)$,O为椭圆的对称中心,F为椭圆的一个焦点,P为椭圆上一点,PF⊥x轴,PF与椭圆的另一个交点为点Q,△POQ为等腰直角三角形,则椭圆的离心率为( )
A.$\frac{\sqrt{3}}{2}$ B.$\frac{\sqrt{5}-1}{2}$ C.$\frac{\sqrt{3}+1}{2}$ D.$\frac{3}{5}$
(2)已知椭圆$\frac{x^{2}}{a}+\frac{y^{2}}{9}=1(a>9)$长轴的一个顶点到直线x - $\sqrt{3}y$ = 0的距离不小于2,则椭圆的离心率的取值范围为_________.
A.$\frac{\sqrt{3}}{2}$ B.$\frac{\sqrt{5}-1}{2}$ C.$\frac{\sqrt{3}+1}{2}$ D.$\frac{3}{5}$
(2)已知椭圆$\frac{x^{2}}{a}+\frac{y^{2}}{9}=1(a>9)$长轴的一个顶点到直线x - $\sqrt{3}y$ = 0的距离不小于2,则椭圆的离心率的取值范围为_________.
答案:
巩固练习3 解析:
(1)由题意可知椭圆的焦点在$x$轴,不妨设$F(c,0)$,$P(c,y_0)$,
因为点$P(c,y_0)$在椭圆上,
所以$\frac{c^{2}}{a^{2}}+\frac{y_0^{2}}{b^{2}}=1$,解得$y_0=\pm\frac{b^{2}}{a}$,所以$P(c,\frac{b^{2}}{a})$,
又$\triangle POQ$为等腰直角三角形,所以$|PF| = |OF|$,
即$\frac{b^{2}}{a}=c$,即$a^{2}-c^{2}=ac$,所以$e^{2}+e - 1 = 0$,
解得$e=\frac{\sqrt{5}-1}{2}$或$e=\frac{-1-\sqrt{5}}{2}$(舍).故选B.
(2)长轴的顶点为$(\pm\sqrt{a},0)$,故$\frac{|\sqrt{a}-0|}{2}\geqslant2$即$a\geqslant16$,
故离心率$e=\sqrt{\frac{a - 9}{a}}=\sqrt{1-\frac{9}{a}}\in[\frac{\sqrt{7}}{4},1)$.
答案:
(1)B
(2)$[\frac{\sqrt{7}}{4},1)$

巩固练习3 解析:
(1)由题意可知椭圆的焦点在$x$轴,不妨设$F(c,0)$,$P(c,y_0)$,
因为点$P(c,y_0)$在椭圆上,
所以$\frac{c^{2}}{a^{2}}+\frac{y_0^{2}}{b^{2}}=1$,解得$y_0=\pm\frac{b^{2}}{a}$,所以$P(c,\frac{b^{2}}{a})$,
又$\triangle POQ$为等腰直角三角形,所以$|PF| = |OF|$,
即$\frac{b^{2}}{a}=c$,即$a^{2}-c^{2}=ac$,所以$e^{2}+e - 1 = 0$,
解得$e=\frac{\sqrt{5}-1}{2}$或$e=\frac{-1-\sqrt{5}}{2}$(舍).故选B.
(2)长轴的顶点为$(\pm\sqrt{a},0)$,故$\frac{|\sqrt{a}-0|}{2}\geqslant2$即$a\geqslant16$,
故离心率$e=\sqrt{\frac{a - 9}{a}}=\sqrt{1-\frac{9}{a}}\in[\frac{\sqrt{7}}{4},1)$.
答案:
(1)B
(2)$[\frac{\sqrt{7}}{4},1)$

查看更多完整答案,请扫码查看


