《2025年师说高中数学选择性必修第一册》

题型三 斜率与倾斜角的变化关系
【问题探究 3】当直线的倾斜角由 0°逐渐增大到 180°，其斜率如何变化？

答案： 问题探究3 提示：由正切函数图象及单调性，当倾斜角为锐角时，斜率为正，且斜率随着倾斜角的增大而增大；当倾斜角为钝角时，斜率为负，且斜率随着倾斜角的增大而增大.

例 3 （1）已知直线 l 的倾斜角为α，斜率为 k，$\frac{\pi}{4}$≤α≤$\frac{3\pi}{4}$，则斜率 k 的取值范围为（ ）
A. [-1,1]
B. (-∞,-1]
C. [1,+∞)
D. (-∞,-1]∪[1,+∞)
（2）已知直线 l 的斜率 k∈[-1,$\sqrt{3}$]，则该直线的倾斜角α的取值范围为（ ）
A. [$\frac{\pi}{3}$,$\frac{3\pi}{4}$]
B. [0,$\frac{\pi}{3}$]∪[$\frac{3\pi}{4}$,π)
C. [$\frac{\pi}{6}$,$\frac{3\pi}{4}$]
D. [0,$\frac{\pi}{6}$]∪[$\frac{3\pi}{4}$,π)

答案： 例3 解析：
(1)由于$\frac{\pi}{4}\leq\alpha\leq\frac{3\pi}{4}$，且k＝tanα，
所以k≥1或k≤－1.故选D.
(2)直线倾斜角为α，则α∈[0，π)，由－1≤k≤$\sqrt{3}$可得－1≤tanα≤$\sqrt{3}$，所以α∈$[0,\frac{\pi}{3}]\cup[\frac{3\pi}{4},\pi)$.故选B.
答案：
(1)D
(2)B

巩固练习 3 （1）已知直线 l₁，l₂，l₃的倾斜角分别为 30°，53°，125°，斜率分别为 k₁，k₂，k₃，则（ ）
A. k₁＜k₂＜k₃
B. k₂＜k₁＜k₃
C. k₃＜k₁＜k₂
D. k₃＜k₂＜k₁
（2）若直线斜率的绝对值等于$\sqrt{3}$，则直线的倾斜角为（ ）
A. 60°
B. 30°
C. 120°
D. 60°或 120°

答案： 巩固练习3 解析：
(1)$k_3=\tan125^{\circ}＜0$，0＜$k_1=\tan30^{\circ}＜k_2=\tan53^{\circ}$，所以$k_3＜k_1＜k_2$.故选C.
(2)当斜率k＝$\sqrt{3}$时，倾斜角为α＝60°；当斜率k＝－$\sqrt{3}$时，倾斜角为α＝120°.故选D.
答案：
(1)C
(2)D

随堂练习
1. 经过 A(0,$\sqrt{3}$)，B(3,0)两点的直线的倾斜角为（ ）
A. $\frac{5\pi}{6}$
B. $\frac{\pi}{6}$
C. $\frac{2\pi}{3}$
D. $\frac{\pi}{3}$

答案： 解析：由题意得$k_{AB}=\frac{0 - \sqrt{3}}{3 - 0}=-\frac{\sqrt{3}}{3}$，所以直线的倾斜角为$\frac{5\pi}{6}$.故选A.
答案：A

2. 斜率为$\frac{1}{3}$的直线的倾斜角α所在的范围是（ ）
A. 0°＜α＜45°
B. 45°＜α＜90°
C. 90°＜α＜135°
D. 135°＜α＜180°

答案： 解析：由题意tanα＝$\frac{1}{3}$，而0°≤α＜180°，所以0°＜α＜45°.故选A.
答案：A

3. 已知直线 l 的一个方向向量为(3,-$\sqrt{3}$)，则直线 l 的倾斜角α = （ ）
A. 30°
B. 60°
C. 120°
D. 150°

答案： 解析：因为直线l的一个方向向量为(3，－$\sqrt{3}$)，所以直线l的斜率为$k=\frac{-\sqrt{3}}{3}=\tan\alpha$，0°≤α＜180°，从而直线l的倾斜角α＝150°.故选D.
答案：D

4. 一束光线射到 x 轴上并经 x 轴反射. 已知入射光线的倾斜角α₁ = 30°，则反射光线的倾斜角α₂ = ________.

答案：
解析：作出入射光线和反射光线，如图.因为入射光线的倾斜角α1＝30°，所以入射角为60°.

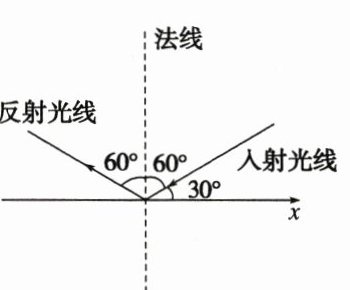
又反射角等于入射角，由图易知，反射光线的倾斜角为60°＋60°＋30°＝150°.
答案：150°