《2025年亮点给力提优课时作业本六年级数学下册苏教版江苏专版》

1. 在括号里填合适的数或单位。
8L70mL=(　　　)L=(　　　)mL
9.3m³=(　　　)m³(　　　)dm³
一个集装箱的容积约是40(　　　)。
一个水壶的容积约是1.5(　　　)。

答案： 8.07 8070 9 300 立方米 升

2. (1)（新素养 几何直观）如图，把长6厘米、宽4厘米的长方形绕对称轴旋转一周，形成的立体图形的表面积是(　　　)平方厘米，体积是(　　　)立方厘米。
　　　　　　　　　　　　　　　

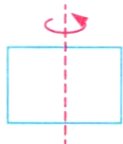
答案：
(1) 131.88 113.04

(2)如图(单位：厘米)，一个立体图形从正面看到的是图①，从上面看到的是图②，这个立体图形的体积是(　　　)立方厘米。如果用一个长方体(或正方体)盒子包装它，那么这个盒子的容积至少是(　　　)立方厘米。
　　　　　　

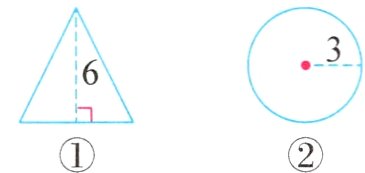
答案：
(2) 56.52 216

(3)如图，将一个表面积是160平方厘米的大长方体在顶点处挖去一个小正方体，则剩下的图形的表面积是(　　　)平方厘米，体积是(　　　)立方厘米。
　　　　　　　　　　　　

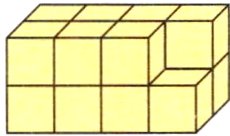
答案：
(3) 160 120

3. 一个圆锥形煤堆高1.2米，底面周长是12.56米。若每立方米煤重1.17吨，这堆煤共重多少吨？(得数保留两位小数)

答案： 12.56÷3.14÷2 = 2(米) $\frac{1}{3}×3.14×2^{2}×1.2 = 5.024$(立方米) 5.024×1.17≈5.88(吨)

4. （新素养 推理意识）如图，把若干张圆形纸片摞起来可以形成圆柱，把圆柱的底面积乘高可以得到圆柱的体积。把若干张同样的直角三角形纸片摞起来形成的物体叫三棱柱，请你推测一下，图中三棱柱的体积是(　　　)立方厘米。
　　　　　

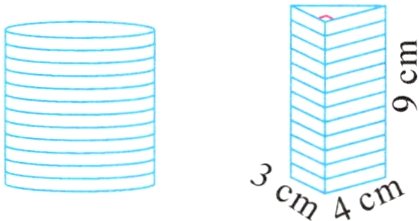
答案： 54 解析：根据圆柱的体积公式，可知三棱柱的体积 = 底面积×高，即 3×4÷2×9 = 54(立方厘米)。

5. 将一块长、宽、高分别为18厘米、12厘米和10厘米的长方体木料削成一个最大的圆柱，这个圆柱的体积是多少立方厘米？

答案： $3.14×(10÷2)^{2}×18 = 1413($立方厘米)

6. （亮点原创）正方体的棱长为6厘米，从它的上、下、前、后、左、右面中心各挖掉一个棱长为1厘米的小正方体，则此时该物体的表面积是(　　　)平方厘米。

答案： 240 解析：大正方体的每个面上都多出 4 个小正方形面，该物体的表面积为 6×6×6 + 1×1×4×6 = 240(平方厘米)。

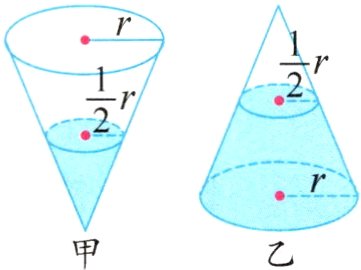
7. 如图，两个相同的圆锥形容器中各装有一些水，水深都是圆锥高的一半，甲、乙两容器中哪一个的水多？多的容器中的水是少的水的几倍？

答案： 设圆锥的高为 6，底面半径为 4。甲容器中水的体积为：$π×(4÷2)^{2}×(6÷2)×\frac{1}{3}=4π$ 乙容器中水的体积为：$π×4^{2}×6×\frac{1}{3}-4π = 28π$ (28π)÷(4π)=7 乙容器中水多，是甲容器中水的 7 倍。