《2025年亮点给力提优课时作业本六年级数学下册苏教版江苏专版》

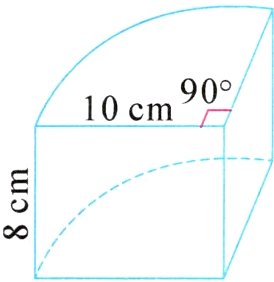
3. 新素养 几何直观 一块蛋糕如图，在它的表面涂上奶油(下底面不涂)，需要涂多少平方厘米的奶油? 这块蛋糕的体积是多少立方厘米?
　　　　　　　　　　　

答案： $3.14\times10^{2}\times\frac{1}{4}+3.14\times10\times2\times8\times\frac{1}{4}+10\times8\times2 = 364.1$（平方厘米） $3.14\times10^{2}\times8\times\frac{1}{4}=628$（立方厘米）

4. 蜂窝煤是由无烟煤制成的。每个蜂窝煤有12个相同的空心小圆柱，如图①。
　
(1)制作一个蜂窝煤需要用无烟煤多少立方厘米? 下面计算方法中，错误的是(　　　)。(填序号)
① 大圆柱的体积 - 12个小圆柱的体积
② 蜂窝煤的底面积×高
③ (大圆柱的底面周长 - 12个小圆柱的底面周长之和)×高
(2)如图②，现有一个圆锥形煤堆，用这堆煤可以制作多少个蜂窝煤?

答案： （1）③ （2）$3.14\times(12\div2)^{2}\times10 - 3.14\times(2\div2)^{2}\times10\times12 = 753.6$（立方厘米） $3.14\times(4\div2)^{2}\times0.9\times\frac{1}{3}=3.768$（立方米） 3.768立方米 = 3768000立方厘米 $3768000\div753.6 = 5000$（个）

5. 如图，亮亮准备用一张边长为24厘米的正方形卡纸做一个尽可能大的圆柱形笔筒。(π取3)
　　　　　　　　　　　　
(1)做成的圆柱形笔筒的体积是多少?
(2)剩余边角料(涂色部分)的面积是多少?

答案： （1）当圆柱形笔筒的高为24厘米时，底面直径为$24\div(1 + 3)=6$（厘米），体积为$3\times(6\div2)^{2}\times24 = 648$（立方厘米）。当圆柱形笔筒的底面周长为24厘米时，底面直径为$24\div3 = 8$（厘米），高为$24 - 8 = 16$（厘米），体积为$3\times(8\div2)^{2}\times16 = 768$（立方厘米）。 $648＜768$ 做成的圆柱形笔筒的体积是768立方厘米。 （2）$24\times8 - 3\times(8\div2)^{2}=144$（平方厘米）

6. 亮点原创 李师傅向下面左图形状的空容器(由上、下两个圆柱组成)中匀速注油，直至注满。注油过程中，容器中油的高度与所用时间的关系如下面右图。
　　
(1)把容器下面的大圆柱注满需(　　　)分钟。
(2)上面的小圆柱高(　　　)厘米。
(3)如果下面的大圆柱底面积是48平方厘米，那么大圆柱的体积是多少立方厘米? 上面小圆柱的底面积是多少平方厘米?

答案： （1）$\frac{4}{3}$ （2）30 （3）$48\times20 = 960$（立方厘米） $960\div\frac{4}{3}\times(2-\frac{4}{3}) = 480$（立方厘米） $480\div30 = 16$（平方厘米） 解析：大圆柱的体积用底面积乘高求得是$48\times20 = 960$（立方厘米）。要求小圆柱的体积，先求出每分钟注油的体积为$960\div\frac{4}{3}=720$（立方厘米），根据注油时间求出小圆柱的体积为$720\times(2-\frac{4}{3}) = 480$（立方厘米），最后求出小圆柱的底面积是$480\div30 = 16$（平方厘米）。