《2025年亮点给力提优课时作业本六年级数学下册苏教版江苏专版》

(2) 小齐用卷笔刀削铅笔，把铅笔的尖端削成圆锥形，削后铅笔的圆柱部分的长度是圆锥部分的9倍，那么圆锥部分的体积是削后铅笔体积的(　　　)。
A. $\frac{1}{3}$
B. $\frac{1}{9}$
C. $\frac{1}{27}$
D. $\frac{1}{28}$

答案： D

8. 一个圆柱形无盖铁皮水桶的高是45 cm，底面直径是40 cm。做这样一个水桶至少需要(　　　)$cm^{2}$的铁皮。

答案： 6908

9. 一根圆柱形铁皮水管，底面直径是10 cm，长是20 cm，做这根圆柱形铁皮水管所用铁皮的面积是(　　　)$cm^{2}$。(接头处忽略不计)

答案： 628

10. 将一个圆锥从顶点沿高切开，其表面积比原来增加了60 $cm^{2}$。若圆锥的高是6 cm，则圆锥的体积是(　　　)$cm^{3}$。

答案： 157 解析：将一个圆锥从顶点沿高切开，表面积就比原来多了两个相同的等腰三角形的面积，这个等腰三角形的底等于圆锥的底面直径，高等于圆锥的高，所以圆锥的底面半径是$60\div2\times2\div6\div2 = 5$(cm)，圆锥的体积就是$\frac{1}{3}\times3.14\times5^{2}\times6 = 157(cm^{3})$。

11. 把一个圆柱按图①的方式沿底面直径和高切成两个半圆柱，表面积会增加40 $cm^{2}$，按图②的方式切成两个圆柱，表面积会增加25.12 $cm^{2}$，求这个圆柱的体积。
　　　　　　　　　　　

答案： $25.12\div2\div3.14 = 4(cm^{2})$ $4 = 2\times2$ $40\div2\div(2\times2) = 5$(cm) $3.14\times2^{2}\times5 = 62.8(cm^{3})$

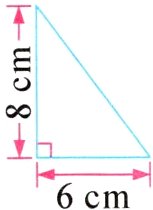
12. 有一个直角三角形(如图)，分别绕它的两条直角边所在的直线旋转一周，能够形成两个大小不同的圆锥。它们的体积各是多少立方厘米？

答案： $\frac{1}{3}\times3.14\times6^{2}\times8 = 301.44$(立方厘米) $\frac{1}{3}\times3.14\times8^{2}\times6 = 401.92$(立方厘米)

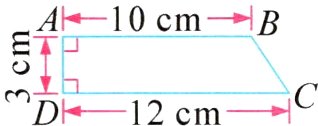
13. 将下面的直角梯形以边AB所在的直线为轴旋转一周，形成的立体图形的体积是多少立方厘米？
　　　　　　　　　　

答案： $3.14\times3^{2}\times12-\frac{1}{3}\times3.14\times3^{2}\times(12 - 10) = 320.28$(立方厘米) 解析：将直角梯形以边AB所在的直线为轴旋转一周，得到的是一个不规则的立体图形，这个立体图形的体积相当于一个底面半径为3厘米、高为12厘米的圆柱体积减去一个底面半径为3厘米、高为$12 - 10 = 2$(厘米)的圆锥的体积，即$3.14\times3^{2}\times12-\frac{1}{3}\times3.14\times3^{2}\times(12 - 10)$
$= 320.28$(立方厘米)。

14. 新情境 知识科普 单板滑雪U型池赛是冬奥会的比赛项目，比赛在一个形状类似于U型的滑道里进行，结构由宽阔平坦的底部和两侧的四分之一的圆管组成(模型图和截面图如下)。请计算下面U型池面的面积。
　　　　　　　

答案： $3.14\times3\times2\times20\times\frac{1}{2}+20\times9 = 368.4(m^{2})$