《2025年亮点给力提优课时作业本六年级数学下册苏教版江苏专版》

1. 一个圆锥的底面半径是4分米，高是6分米，它的底面积是(　　　)平方分米，体积是(　　　)立方分米。

答案： 50.24 100.48

2. 一个圆柱和一个圆锥的底面积相等，体积也相等。若圆柱的高是1.2分米，则圆锥的高是(　　　)分米；若圆锥的高是1.2分米，则圆柱的高是(　　　)分米。

答案： 3.6 0.4

3. 一个圆柱和一个圆锥等底等高，体积相差18立方厘米。圆柱的体积是(　　　)立方厘米，圆锥的体积是(　　　)立方厘米。

答案： 27 9

4. 亮点原创 右图圆柱形容器内的水占圆柱形容器容积的$\frac{1}{3}$，倒入圆锥形容器(　　　)内正好倒满。（单位：cm）
　

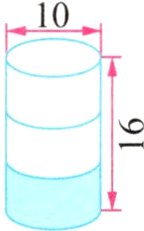
答案： A

5. 如图，打麦场上堆有一堆小麦。
　　　　　
(1) 这个小麦堆的占地面积是(　　　)平方米。
(2) 如果每立方米小麦约重0.8吨，那么用一辆载质量6吨的卡车最少运多少次可以运完?

答案： （1）78.5 （2）$78.5×3×\frac{1}{3}×0.8÷6\approx11$（次）

6. 把一个棱长为6分米的正方体木料削成一个最大的圆锥，需要削去(　　　)立方分米的木料。

答案： 159.48

7. 鞍山玉佛山书画院是鞍山唯一的一座水上书画院，其设计可以近似看成一个圆柱和圆锥的组合体。奇奇用橡皮泥制作了一个模型(如图)，已知圆锥部分与圆柱部分高之比为9:7，该模型的总体积为274.75 cm³，模型中圆锥部分的高是多少?

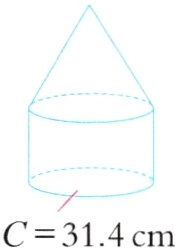
答案： 圆锥部分与圆柱部分体积之比为$(9÷3):7 = 3:7$ $274.75×\frac{3}{3 + 7}=82.425(cm^{3})$ $31.4÷3.14÷2 = 5(cm)$ $82.425×3÷(3.14×5^{2}) = 3.15(cm)$

8. 如图，瓶底的面积与杯口的面积相等，将瓶中的液体倒入杯子中，能倒满(　　　)杯。
　　　　　　　　　　　　　
A. 2
B. 3
C. 6
D. 8

答案： C

9. 如图，一个圆锥形容器中装有3升水，水面高度正好是圆锥形容器高度的$\frac{1}{2}$，这个容器的容积是多少升?（忽略容器壁厚度）

答案： $\frac{1}{2}r:r = 1:2$ $\frac{1}{2}h:h = 1:2$ $V_{小}:V_{大}=(1^{2}×1×\frac{1}{3}):(2^{2}×2×\frac{1}{3}) = 1:8$ $3×8 = 24$（升） 解析：根据水面的高度与容器的高度的比为$1:2$，水面半径和容器底面半径的比为$1:2$，可得水的体积与容器的容积的比为$(1^{2}×1×\frac{1}{3}):(2^{2}×2×\frac{1}{3}) = 1:8$，这个容器的容积就是$3×8 = 24$（升）。