《2025年亮点给力提优课时作业本六年级数学下册苏教版江苏专版》

1. 一个圆柱形油桶的底面积是1.2平方米，高是0.5米，这个油桶的体积是（ ）立方米。

答案： 0.6

2. 如图，把一根20厘米长的圆柱形木料沿横截面切开，表面积增加了100平方厘米，原来这根木料的体积是（ ）立方厘米。
　　　　　　

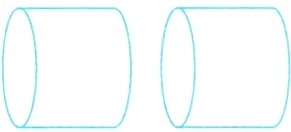
答案： 1000

3. 如图，圆柱的底面半径是6cm，高是10cm。小明没直接用体积公式计算圆柱的体积，而是根据圆柱体积的计算公式的推导过程，分三步计算该圆柱的体积。
　　　　　
第一步：$2×3.14×6×10 = 376.8( cm^{2})$。
第二步：$376.8÷2 = 188.4( cm^{2})$。
请你补充第三步：（ ）。

答案： $188.4×6 = 1130.4(cm^{2})$

4. 选一选。
（1）一个圆柱形油桶的体积（ ）它的容积。
A. 小于
B. 大于
C. 等于

答案：
(1) B

（2）把一个棱长为6厘米的正方体削成一个最大的圆柱，这个圆柱的体积是（ ）立方厘米。
A. $6\pi$
B. $54\pi$
C. $36\pi$

答案：
(2) B

5. 新素养 创新意识 有一种圆形古代钱币，其直径为4厘米，厚度为2毫米，正中间的正方形缺口的边长为1厘米。把20枚这样的钱币对齐正方形缺口垒起来，则垒起来的钱币的体积是（ ）立方厘米。

答案： 46.24

6. 一个底面周长是188.4厘米的圆柱形玻璃鱼缸内装有适量的水。将一些水草、小石块和金鱼放到水中（水未溢出），水面上升了4厘米，这些水草、小石块和金鱼的体积一共是多少立方厘米？

答案： $188.4÷3.14÷2 = 30$（厘米） $3.14×30^{2}×4 = 11304$（立方厘米）

7. 亮点原创 甲、乙两个圆柱形水杯，底面半径的比是2∶3，高的比是2∶1。将甲水杯装满水后全部倒入乙水杯，乙水杯中水面距杯口1.6cm。甲水杯的高度是（ ）cm，乙水杯的高度是（ ）cm。（忽略玻璃的厚度）

答案： 28.8 14.4 解析 根据甲、乙两个水杯的底面半径的比是 $2:3$ 和高的比是 $2:1$，得到甲、乙两个水杯的体积比为 $8:9$。甲水杯装满水设为 8 份，倒入乙水杯后，距杯口还有 1 份的水，那么 1 份水的高度就是 1.6 cm，则乙水杯的高度为 $1.6×9 = 14.4(cm)$，甲水杯的高度为 $14.4×2 = 28.8(cm)$。

8. 新素养 推理意识 如图，一个油瓶内部深30厘米，底面内直径是10厘米。瓶里油深15厘米，把瓶盖拧紧后，使其瓶口向下倒立，这时油深25厘米。油瓶的容积是多少毫升？

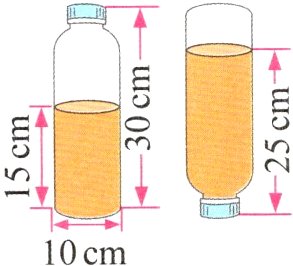
答案： $3.14×(10÷2)^{2}×(30 - 25 + 15)$
$= 1570$（立方厘米） 1570 立方厘米 = 1570 毫升
解析 因为油瓶的大小和形状没有发生变化，油瓶里的油也没有发生变化，所以倒置前后油的体积是相同的，空余部分的体积也是相同的，因此这个油瓶的容积 = 油的体积 + 空余部分的体积，把倒置前油瓶里的油的体积和倒置后油瓶里空余部分的体积相加，就可以求出这个油瓶的容积。