《2025年亮点给力提优课时作业本六年级数学下册苏教版江苏专版》

例2 如图，在四边形ABCD中，AO：OC = 3：2，BO：OD = 5：3。那么$S_{\triangle ABD}：S_{\triangle BCD}=$(　　　)，$S_{\triangle ABC}：S_{\triangle ACD}=$(　　　)。（填最简单的整数比）
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
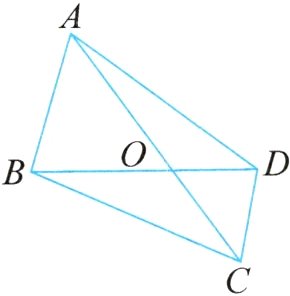
我的思考 要想算出△ABD与△BCD的面积之比，可以根据等高模型直接算出组成△ABD的小三角形（△AOB与△AOD）和组成△BCD的小三角形（△COB与△COD）的比例关系。$\frac{S_{\triangle AOB}}{S_{\triangle COB}}=\frac{S_{\triangle AOD}}{S_{\triangle COD}}=\frac{AO}{OC}$，则$\frac{S_{\triangle AOB}+S_{\triangle AOD}}{S_{\triangle COB}+S_{\triangle COD}}=\frac{AO}{OC}$，即$\frac{S_{\triangle ABD}}{S_{\triangle BCD}}=\frac{AO}{OC}$。$\frac{S_{\triangle AOB}}{S_{\triangle AOD}}=\frac{S_{\triangle COB}}{S_{\triangle COD}}=\frac{BO}{OD}$，则$\frac{S_{\triangle AOB}+S_{\triangle COB}}{S_{\triangle AOD}+S_{\triangle COD}}=\frac{BO}{OD}$，即$\frac{S_{\triangle ABC}}{S_{\triangle ACD}}=\frac{BO}{OD}$。也可以采用假设法，假设$S_{\triangle AOB}=15$，因为AO：OC = 3：2，所以$S_{\triangle AOB}：S_{\triangle BOC}=3：2$，则$S_{\triangle BOC}=\frac{2}{3}\times15 = 10$，又因为BO：OD = 5：3，所以$S_{\triangle AOB}：S_{\triangle AOD}=S_{\triangle BOC}：S_{\triangle COD}=5：3$，则$S_{\triangle AOD}=\frac{3}{5}\times15 = 9$，$S_{\triangle COD}=\frac{3}{5}\times10 = 6$，所以$S_{\triangle ABD}：S_{\triangle BCD}=(15 + 9)：(10 + 6)=24：16 = 3：2$，$S_{\triangle ABC}：S_{\triangle ACD}=(15 + 10)：(9 + 6)=25：15 = 5：3$。
我的解答

答案： 我的解答：$3:2$，$5:3$

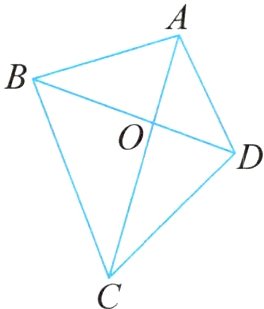
活学活用 如图，在四边形ABCD中，BO：OD = 3：2，△ABC的面积为51平方厘米，则△DAC的面积为多少平方厘米？
　　

答案： 活学活用：$BO:OD = 3:2$，$S_{\triangle AOB}:S_{\triangle OAD}=3:2$，$S_{\triangle BOC}:S_{\triangle COD}=3:2$，$(S_{\triangle AOB}+S_{\triangle BOC}):(S_{\triangle OAD}+S_{\triangle COD})=S_{\triangle ABC}:S_{\triangle DAC}=3:2$，$S_{\triangle DAC}=\frac{2}{3}\times51 = 34$(平方厘米)

甲、乙两个圆柱形容器，底面积之比为5：3，甲容器中水深9厘米，乙容器中水深3厘米，现在往两个容器中注入同样多的水，使它们的水深相等。那么甲容器中的水面上升了多少厘米？

答案： 甲、乙两容器中水面上升的高度比：$3:5$，甲容器中水面上升高度：$(9 - 3)\div(5 - 3)\times3 = 9$(厘米)。解析：由甲、乙两个容器的底面积之比为$5:3$和注入同样多的水可知，甲、乙两个容器中水面上升的高度比为$(1\div5):(1\div3)=3:5$，再结合原来两个容器中水深相差$9 - 3 = 6$(厘米)解决问题。