8.(河北中考)图 $ 1 $ 是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图 $ 2 $ 所示,此时液面 $ AB = $ ( )
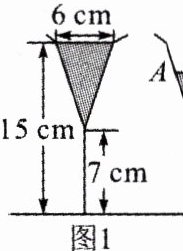
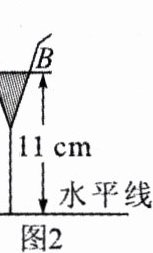
A. $ 1 $ cm
B. $ 2 $ cm
C. $ 3 $ cm
D. $ 4 $ cm


A. $ 1 $ cm
B. $ 2 $ cm
C. $ 3 $ cm
D. $ 4 $ cm
答案:
C
9.(陕西中考)小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高. 如图所示,在某一时刻,他们在阳光下,分别测得该建筑物 $ OB $ 的影长 $ OC $ 为 $ 16 $ 米,$ OA $ 的影长 $ OD $ 为 $ 20 $ 米,小明的影长 $ FG $ 为 $ 2.4 $ 米,其中 $ O $,$ C $,$ D $,$ F $,$ G $ 五点在同一直线上,$ A $,$ B $,$ O $ 三点在同一直线上,且 $ AO \perp OD $,$ EF \perp FG $. 已知小明的身高 $ EF $ 为 $ 1.8 $ 米,求旗杆的高 $ AB $.


答案:
因为AD//EG,所以∠ADO = ∠EGF。因为∠AOD = ∠EFG = 90°,所以△AOD∽△EFG,所以$\frac{AO}{EF}=\frac{OD}{FG}$,即$\frac{AO}{1.8}=\frac{20}{2.4}$,所以AO = 15米。同理得△BOC∽△AOD,所以$\frac{BO}{AO}=\frac{OC}{OD}$,即$\frac{BO}{15}=\frac{16}{20}$,BO = 12米,所以AB = AO - BO = 15 - 12 = 3(米),答:旗杆的高度AB为3米
10.(2024·自贡)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
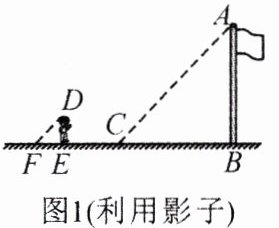
(1)如图 $ 1 $,小张在测量时发现,自己在操场上的影长 $ EF $ 恰好等于自己的身高 $ DE $. 此时,小组同学测得旗杆 $ AB $ 的影长 $ BC $ 为 $ 11.3 $ m,据此可得旗杆高度为______ m;
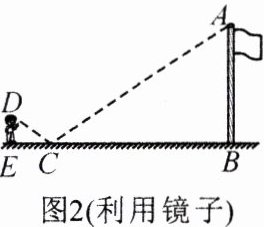
(2)如图 $ 2 $,小李站在操场上 $ E $ 点处,前面水平放置镜面 $ C $,并通过镜面观测到旗杆顶部 $ A $. 小组同学测得小李的眼睛距地面高度 $ DE = 1.5 $ m,小李到镜面距离 $ EC = 2 $ m,镜面到旗杆的距离 $ CB = 16 $ m. 求旗杆高度;
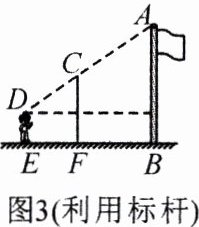
(3)小王所在小组采用图 $ 3 $ 的方法测量,结果误差较大. 在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度. 方法如下:
如图 $ 4 $,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面 $ M $,$ N $ 两点始终处于同一水平线上.
如图 $ 5 $,在支架上端 $ P $ 处,用细线系小重物 $ Q $,标高线 $ PQ $ 始终垂直于水平地面.
如图 $ 6 $,在江姐故里广场上 $ E $ 点处,同学们用注水管确定与雕塑底部 $ B $ 处于同一水平线的 $ D $,$ G $ 两点,并标记观测视线 $ DA $ 与标高线交点 $ C $,测得标高 $ CG = 1.8 $ m,$ DG = 1.5 $ m. 将观测点 $ D $ 后移 $ 24 $ m 到 $ D' $ 处. 采用同样方法,测得 $ C'G' = 1.2 $ m,$ D'G' = 2 $ m. 求雕塑高度(结果精确到 $ 1 $ m).




(1)如图 $ 1 $,小张在测量时发现,自己在操场上的影长 $ EF $ 恰好等于自己的身高 $ DE $. 此时,小组同学测得旗杆 $ AB $ 的影长 $ BC $ 为 $ 11.3 $ m,据此可得旗杆高度为______ m;
(2)如图 $ 2 $,小李站在操场上 $ E $ 点处,前面水平放置镜面 $ C $,并通过镜面观测到旗杆顶部 $ A $. 小组同学测得小李的眼睛距地面高度 $ DE = 1.5 $ m,小李到镜面距离 $ EC = 2 $ m,镜面到旗杆的距离 $ CB = 16 $ m. 求旗杆高度;
(3)小王所在小组采用图 $ 3 $ 的方法测量,结果误差较大. 在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度. 方法如下:
如图 $ 4 $,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面 $ M $,$ N $ 两点始终处于同一水平线上.
如图 $ 5 $,在支架上端 $ P $ 处,用细线系小重物 $ Q $,标高线 $ PQ $ 始终垂直于水平地面.
如图 $ 6 $,在江姐故里广场上 $ E $ 点处,同学们用注水管确定与雕塑底部 $ B $ 处于同一水平线的 $ D $,$ G $ 两点,并标记观测视线 $ DA $ 与标高线交点 $ C $,测得标高 $ CG = 1.8 $ m,$ DG = 1.5 $ m. 将观测点 $ D $ 后移 $ 24 $ m 到 $ D' $ 处. 采用同样方法,测得 $ C'G' = 1.2 $ m,$ D'G' = 2 $ m. 求雕塑高度(结果精确到 $ 1 $ m).

答案:
11.3@@由反射定律可知,∠DCE = ∠ACB,又∠DEC = 90° = ∠ABC,所以△DEC∽△ABC,所以$\frac{AB}{DE}=\frac{BC}{CE}$,即$\frac{AB}{1.5}=\frac{16}{2}$,解得AB = 12,所以旗杆高度为12米@@因为∠CDG = ∠ADB,∠CGD = 90° = ∠ABD,所以△DCG∽△DAB,所以$\frac{CG}{AB}=\frac{DG}{BD}$。设AB = x m,BD = y m,则$\frac{1.8}{x}=\frac{1.5}{y}$,所以$y=\frac{5}{6}x$。同理可得$\frac{C'G'}{AB}=\frac{D'G'}{D'B}$,所以$\frac{1.2}{x}=\frac{2}{24 + y}$,即$\frac{1.2}{x}=\frac{2}{24+\frac{5}{6}x}$,解得x = 28.8;经检验,x = 28.8是原方程的解,故AB≈29 m,所以雕塑高度AB约为29 m
查看更多完整答案,请扫码查看


