《2025年原创新课堂九年级数学下册人教版》

1. 如图所示，某校数学兴趣小组利用标杆 $ BE $ 测量建筑物的高度，已知标杆 $ BE $ 高 $ 1.5 $ m，测得 $ AB = 1.2 $ m，$ BC = 12.8 $ m，则建筑物 $ CD $ 的高是 （ ）

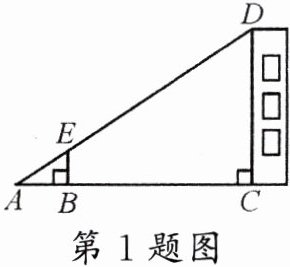
A. $ 17.5 $ m
B. $ 17 $ m
C. $ 16.5 $ m
D. $ 18 $ m

答案： A

2.（2024·南阳月考）如图，数学活动课上，为测量学校旗杆高度，小菲同学在脚下水平放置一平面镜，然后向后退（保持脚、镜和旗杆底端在同一直线上），直到她刚好在镜子中看到旗杆的顶端. 已知小菲的眼睛离地面高度为 $ 1.6 $ m，同时量得小菲与镜子的水平距离为 $ 2 $ m，镜子与旗杆的水平距离为 $ 10 $ m，则旗杆高度为______.

答案： 8 m

3. 如图，小明同学用自制的直角三角形纸板 $ DEF $ 测量树的高度 $ AB $，他调整自己的位置，设法使斜边 $ DF $ 保持水平，并且边 $ DE $ 与点 $ B $ 在同一直线上，已知纸板的两条边 $ DF = 50 $ cm，$ DE = 40 $ cm，测得边 $ DF $ 离地面的高度 $ AC = 1.5 $ m，$ CD = 12 $ m，求树高 $ AB $.

答案： 在Rt△DEF中，$DE^{2}+EF^{2}=DF^{2}$，即$40^{2}+EF^{2}=50^{2}$，所以$EF = 30$。由题意得∠BCD = ∠DEF = 90°，∠CDB = ∠EDF，所以△DCB∽△DEF，所以$\frac{BC}{EF}=\frac{DC}{DE}$。因为EF = 30 cm = 0.3 m，DE = 40 cm = 0.4 m，CD = 12 m，所以$\frac{BC}{0.3}=\frac{12}{0.4}$，解得BC = 9 m。因为AC = 1.5 m，所以AB = AC + BC = 1.5 + 9 = 10.5(m)

4. 如图，某零件的外径为 $ 10 $ cm，用一个交叉卡钳（两条尺长 $ AC $ 和 $ BD $ 相等）可测量零件的内孔直径 $ AB $. 如果 $ OA:OC = OB:OD = 3 $，且量得 $ CD = 3 $ cm，则零件的厚度 $ x $ 为 （ ）

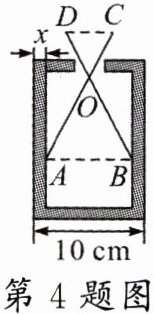
A. $ 0.3 $ cm
B. $ 0.5 $ cm
C. $ 0.7 $ cm
D. $ 1 $ cm

答案： B

5.（教材 $ P40 $ 例 $ 5 $ 变式）如图，一条河的两岸有一段是平行的，在河的南岸边每隔 $ 5 $ 米有一棵树，在北岸边每隔 $ 60 $ 米有一根电线杆. 小丽站在离南岸边 $ 15 $ 米的点 $ P $ 处看北岸，发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住，并且在这两棵树之间还有三棵树，则河宽为______米.

答案： 30

6.（2024·郑州管城区模拟）两千四百多年前，我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因，图①是小孔成像实验图，抽象为数学问题如图②：$ AC $ 与 $ BD $ 交于点 $ O $，$ AB // CD $，若点 $ O $ 到 $ AB $ 的距离为 $ 10 $ cm，点 $ O $ 到 $ CD $ 的距离为 $ 15 $ cm，蜡烛火焰 $ AB $ 的高度是 $ 3 $ cm，则蜡烛火焰倒立的像 $ CD $ 的高度是 （ ）

A. $ 5 $ cm
B. $ 4.5 $ cm
C. $ 6.5 $ cm
D. $ 8 $ cm

答案： B

7. 如图，现要对 $ \triangle ABC $ 空地进行绿化，中位线 $ MN $ 把 $ \triangle ABC $ 空地分割成两部分，其中 $ \triangle AMN $ 部分种植红花，四边形 $ BCNM $ 部分种植绿草，已知红花的种植面积是 $ 20 $ $ m^{2} $，则绿草的种植面积为______ $ m^{2} $.

答案： 60