1.在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为 3,4,5 的三角形按图①的方式向外扩张,得到新三角形,它们的对应边间距为 1,则新三角形与原三角形相似;
乙:将邻边为 3 和 5 的矩形按图②的方式向外扩张,得到新的矩形,它们的对应边间距均为 1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是 ( )
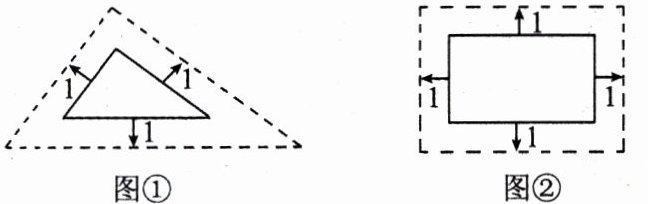
图① 图②
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
甲:将边长为 3,4,5 的三角形按图①的方式向外扩张,得到新三角形,它们的对应边间距为 1,则新三角形与原三角形相似;
乙:将邻边为 3 和 5 的矩形按图②的方式向外扩张,得到新的矩形,它们的对应边间距均为 1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是 ( )

图① 图②
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
答案:
A
2.如图,在四边形 ABCD 与四边形 EFGH 中,∠A = 100°,∠B = 90°,∠C = 120°,∠F = 90°,∠G = 120°,∠H = 50°,则四边形 ABCD 与四边形 EFGH ____________.(填“一定相似”或“不一定相似”)


答案:
不一定相似
3.如图,点 P 在△ABC 的边 AC 上,要判断△ABP∽△ACB,添加一个条件,不正确的是 ( )
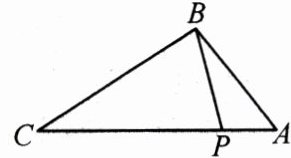
A.∠ABP = ∠C
B.∠APB = ∠ABC
C.$\frac{AP}{AB}=\frac{AB}{AC}$
D.$\frac{AB}{BP}=\frac{AC}{CB}$

A.∠ABP = ∠C
B.∠APB = ∠ABC
C.$\frac{AP}{AB}=\frac{AB}{AC}$
D.$\frac{AB}{BP}=\frac{AC}{CB}$
答案:
D
4.在△ABC 和△A'B'C'中,已知∠A = ∠A',$\frac{AB}{BC}=\frac{A'B'}{B'C'}$,那么△ABC 和△A'B'C' ____________.(填“一定相似”或“不一定相似”)
答案:
不一定相似
5.如图,在△ABC 中,∠C = 90°,∠A = 30°,D 是 AC 的中点,过点 D 沿直线剪下一个与△ABC 相似的小三角形纸板,则不同的剪法共有( )
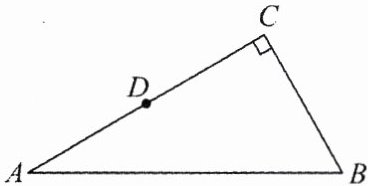
A.1 种
B.2 种
C.3 种
D.4 种

A.1 种
B.2 种
C.3 种
D.4 种
答案:
C
6.如图,在四边形 ABCD 中,AD//BC,∠B = 90°,AB = 12,AD = 4,BC = 9,点 P 是 AB 上一动点.若△PAD 与△PBC 是相似三角形,求 AP 的长.
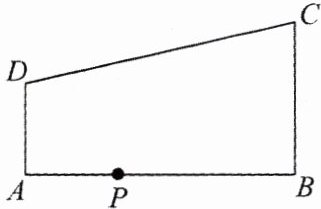

答案:
因为∠B = 90°,AD//BC,所以∠A = 180° - ∠B = 90°,所以∠PAD = ∠PBC = 90°。设AP的长为x,则BP = 12 - x。连接PD,PC。若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:①若△APD∽△BPC,则AP : BP = AD : BC,即x : (12 - x) = 4 : 9,解得x = $\frac{48}{13}$;②若△APD∽△BCP,则AP : BC = AD : BP,即x : 9 = 4 : (12 - x),解得x = 6。综上可知,AP的长为$\frac{48}{13}$或6时,△PAD与△PBC是相似三角形。
查看更多完整答案,请扫码查看


