10.(湘西中考)如图,在$\square ABCD$中,$E$是$AD$边上的中点,连接$BE$,并延长$BE$交$CD$延长线于点$F$,则$\triangle EDF$与$\triangle BCF$的周长之比是 ( )

A.$1:2$
B.$1:3$
C.$1:4$
D.$1:5$

A.$1:2$
B.$1:3$
C.$1:4$
D.$1:5$
答案:
A
11.(贵港中考)如图,在$\triangle ABC$中,$EF// BC$,$AB = 3AE$,若$S_{四边形BCFE}=16$,则$S_{\triangle ABC}=$ ( )

A.$16$
B.$18$
C.$20$
D.$24$

A.$16$
B.$18$
C.$20$
D.$24$
答案:
B
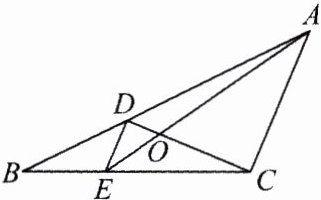
12. 如图,$D$,$E$分别是$\triangle ABC$的边$AB$,$BC$上的点,且$DE// AC$,$AE$,$CD$相交于点$O$.若$S_{\triangle DOE}:S_{\triangle COA}=1:25$,则$S_{\triangle BDE}$与$S_{\triangle CDE}$的比为________.

答案:
$1:4$
13.(杭州中考)如图,在锐角三角形$ABC$中,点$D$,$E$分别在边$AC$,$AB$上,$AG\perp BC$于点$G$,$AF\perp DE$于点$F$,$\angle EAF=\angle GAC$.
(1)求证:$\triangle ADE\backsim\triangle ABC$;
(2)若$AD = 3$,$AB = 5$,求$\frac{AF}{AG}$的值.

(1)求证:$\triangle ADE\backsim\triangle ABC$;
(2)若$AD = 3$,$AB = 5$,求$\frac{AF}{AG}$的值.

答案:
(1) 因为 $AG\perp BC$,$AF\perp DE$,所以 $\angle AFE=\angle AGC = 90^{\circ}$。因为 $\angle EAF=\angle GAC$,所以 $\angle AED=\angle ACB$。因为 $\angle EAD=\angle CAB$,所以 $\triangle ADE\sim\triangle ABC$
(2) 由
(1)知 $\triangle ADE\sim\triangle ABC$,又因为 $AF\perp DE$,$AG\perp BC$,所以 $\frac{AF}{AG}=\frac{AD}{AB}=\frac{3}{5}$
(1) 因为 $AG\perp BC$,$AF\perp DE$,所以 $\angle AFE=\angle AGC = 90^{\circ}$。因为 $\angle EAF=\angle GAC$,所以 $\angle AED=\angle ACB$。因为 $\angle EAD=\angle CAB$,所以 $\triangle ADE\sim\triangle ABC$
(2) 由
(1)知 $\triangle ADE\sim\triangle ABC$,又因为 $AF\perp DE$,$AG\perp BC$,所以 $\frac{AF}{AG}=\frac{AD}{AB}=\frac{3}{5}$
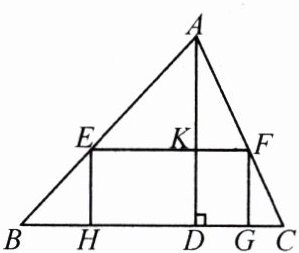
14.已知锐角$\triangle ABC$中,边$BC$长为$12$,高$AD$长为$8$.
(1)如图,矩形$EFGH$的边$GH$在$BC$边上,其余两个顶点$E$,$F$分别在$AB$,$AC$边上,$EF$交$AD$于点$K$.
①求$\frac{EF}{AK}$的值;
②设$EH = x$,矩形$EFGH$的面积为$S$,求$S$与$x$的函数关系式,并求出$S$的最大值;
(2)若$AB = AC$,正方形$PQMN$的两个顶点在$\triangle ABC$一边上,另两个顶点分别在$\triangle ABC$的另两边上,直接写出正方形$PQMN$的边长.
(1)如图,矩形$EFGH$的边$GH$在$BC$边上,其余两个顶点$E$,$F$分别在$AB$,$AC$边上,$EF$交$AD$于点$K$.
①求$\frac{EF}{AK}$的值;
②设$EH = x$,矩形$EFGH$的面积为$S$,求$S$与$x$的函数关系式,并求出$S$的最大值;
(2)若$AB = AC$,正方形$PQMN$的两个顶点在$\triangle ABC$一边上,另两个顶点分别在$\triangle ABC$的另两边上,直接写出正方形$PQMN$的边长.

答案:
(1) ① 因为 $EF// BC$,所以 $\triangle AEF\sim\triangle ABC$,所以 $\frac{AK}{AD}=\frac{EF}{BC}$,所以 $\frac{EF}{AK}=\frac{BC}{AD}=\frac{12}{8}=\frac{3}{2}$,即 $\frac{EF}{AK}$ 的值是 $\frac{3}{2}$ ② 因为 $EH = x$,所以 $KD = EH = x$,$AK = 8 - x$,因为 $\frac{EF}{AK}=\frac{3}{2}$,所以 $EF=\frac{3}{2}(8 - x)$,所以 $S = EH\cdot EF=\frac{3}{2}x(8 - x)=-\frac{3}{2}(x - 4)^2 + 24$,所以当 $x = 4$ 时,$S$ 的最大值是 24
(2) 设正方形的边长为 $a$,① 当正方形 $PQMN$ 的两个顶点在 $BC$ 边上时,$\frac{8 - a}{a}=\frac{8}{12}$,解得 $a=\frac{24}{5}$; ② 当正方形 $PQMN$ 的两个顶点在 $AB$ 或 $AC$ 边上时,因为 $AB = AC$,$AD\perp BC$,所以 $BD = CD = 6$,所以 $AB = AC=\sqrt{AD^{2}+BD^{2}}=\sqrt{6^{2}+8^{2}} = 10$,所以 $AB$ 或 $AC$ 边上的高 $=\frac{AD\cdot BC}{AB}=\frac{8\times12}{10}=\frac{48}{5}$,所以 $\frac{\frac{48}{5}-a}{a}=\frac{\frac{48}{5}}{10}$,解得 $a=\frac{240}{49}$。综上可得,正方形 $PQMN$ 的边长是 $\frac{24}{5}$ 或 $\frac{240}{49}$
(1) ① 因为 $EF// BC$,所以 $\triangle AEF\sim\triangle ABC$,所以 $\frac{AK}{AD}=\frac{EF}{BC}$,所以 $\frac{EF}{AK}=\frac{BC}{AD}=\frac{12}{8}=\frac{3}{2}$,即 $\frac{EF}{AK}$ 的值是 $\frac{3}{2}$ ② 因为 $EH = x$,所以 $KD = EH = x$,$AK = 8 - x$,因为 $\frac{EF}{AK}=\frac{3}{2}$,所以 $EF=\frac{3}{2}(8 - x)$,所以 $S = EH\cdot EF=\frac{3}{2}x(8 - x)=-\frac{3}{2}(x - 4)^2 + 24$,所以当 $x = 4$ 时,$S$ 的最大值是 24
(2) 设正方形的边长为 $a$,① 当正方形 $PQMN$ 的两个顶点在 $BC$ 边上时,$\frac{8 - a}{a}=\frac{8}{12}$,解得 $a=\frac{24}{5}$; ② 当正方形 $PQMN$ 的两个顶点在 $AB$ 或 $AC$ 边上时,因为 $AB = AC$,$AD\perp BC$,所以 $BD = CD = 6$,所以 $AB = AC=\sqrt{AD^{2}+BD^{2}}=\sqrt{6^{2}+8^{2}} = 10$,所以 $AB$ 或 $AC$ 边上的高 $=\frac{AD\cdot BC}{AB}=\frac{8\times12}{10}=\frac{48}{5}$,所以 $\frac{\frac{48}{5}-a}{a}=\frac{\frac{48}{5}}{10}$,解得 $a=\frac{240}{49}$。综上可得,正方形 $PQMN$ 的边长是 $\frac{24}{5}$ 或 $\frac{240}{49}$
查看更多完整答案,请扫码查看


