5. (2024·盐城)如图,点 C 在以 AB 为直径的⊙O 上,过点 C 作⊙O 的切线 l,过点 A 作 AD⊥l,垂足为 D,连接 AC,BC.
(1)求证:△ABC∽△ACD;
(2)若 AC = 5,CD = 4,求⊙O 的半径.
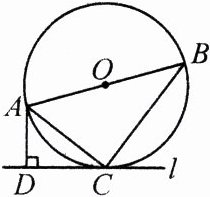
(1)求证:△ABC∽△ACD;
(2)若 AC = 5,CD = 4,求⊙O 的半径.

答案:
(1) 连接OC,因为l是⊙O的切线,所以OC⊥l,因为AD⊥l,所以OC//AD,所以∠CAD = ∠ACO = ∠CAB,因为∠D = ∠ACB = 90°,所以△ABC∽△ACD。
(2) 因为AC = 5,CD = 4,∠ADC = 90°,所以$AD=\sqrt{AC^{2}-CD^{2}} = 3$,因为△ABC∽△ACD,所以$\frac{AB}{AC}=\frac{AC}{AD}$,所以$\frac{AB}{5}=\frac{5}{3}$,所以$AB=\frac{25}{3}$,所以⊙O的半径为$\frac{25}{6}$。
(1) 连接OC,因为l是⊙O的切线,所以OC⊥l,因为AD⊥l,所以OC//AD,所以∠CAD = ∠ACO = ∠CAB,因为∠D = ∠ACB = 90°,所以△ABC∽△ACD。
(2) 因为AC = 5,CD = 4,∠ADC = 90°,所以$AD=\sqrt{AC^{2}-CD^{2}} = 3$,因为△ABC∽△ACD,所以$\frac{AB}{AC}=\frac{AC}{AD}$,所以$\frac{AB}{5}=\frac{5}{3}$,所以$AB=\frac{25}{3}$,所以⊙O的半径为$\frac{25}{6}$。
6. (2024·安阳月考)如图,AB 为⊙O 的直径,C,D 为⊙O 上的两点,且 AC 平分∠BAD,过点 C 作直线 EF⊥AD,交 AD 的延长线于点 E.
(1)试说明:EF 是⊙O 的切线;
(2)若 AE = $\frac{16}{5}$,⊙O 的半径是 $\frac{5}{2}$,求 AC 的长.
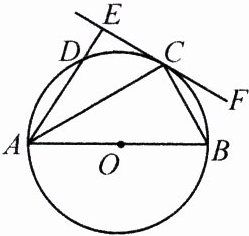
(1)试说明:EF 是⊙O 的切线;
(2)若 AE = $\frac{16}{5}$,⊙O 的半径是 $\frac{5}{2}$,求 AC 的长.

答案:
(1) 连接OC,因为EF⊥AD,所以∠AEC = 90°,因为AC平分∠BAD,所以∠EAC = ∠CAB,因为OA = OC,所以∠CAB = ∠ACO,所以∠EAC = ∠ACO,所以AE//OC,所以∠AEC = ∠OCF = 90°,因为OC是⊙O的半径,所以EF是⊙O的切线。
(2) 因为AB为⊙O的直径,所以∠ACB = 90°,因为∠ACB = ∠AEC = 90°,∠EAC = ∠CAB,所以△AEC∽△ACB,所以$\frac{AE}{AC}=\frac{AC}{AB}$,所以$AC^{2}=AE·AB$,所以$AC^{2}=\frac{16}{5}×5 = 16$,所以AC = 4。
(1) 连接OC,因为EF⊥AD,所以∠AEC = 90°,因为AC平分∠BAD,所以∠EAC = ∠CAB,因为OA = OC,所以∠CAB = ∠ACO,所以∠EAC = ∠ACO,所以AE//OC,所以∠AEC = ∠OCF = 90°,因为OC是⊙O的半径,所以EF是⊙O的切线。
(2) 因为AB为⊙O的直径,所以∠ACB = 90°,因为∠ACB = ∠AEC = 90°,∠EAC = ∠CAB,所以△AEC∽△ACB,所以$\frac{AE}{AC}=\frac{AC}{AB}$,所以$AC^{2}=AE·AB$,所以$AC^{2}=\frac{16}{5}×5 = 16$,所以AC = 4。
7. (2024·无锡)如图,AB 是⊙O 的直径,△ACD 内接于⊙O,$\widehat{CD}$ = $\widehat{DB}$,AB,CD 的延长线相交于点 E,且 DE = AD.
(1)求证:△CAD∽△CEA;
(2)求∠ADC 的度数.
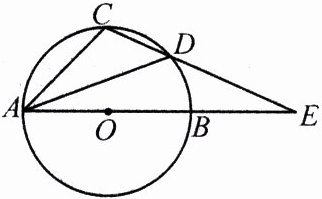
(1)求证:△CAD∽△CEA;
(2)求∠ADC 的度数.

答案:
(1) 因为$\overset{\frown}{CD}=\overset{\frown}{DB}$,所以∠CAD = ∠DAB,因为DE = AD,所以∠DAB = ∠E,所以∠CAD = ∠E,又因为∠C = ∠C,所以△CAD∽△CEA。
(2) 连接BC,因为AB为直径,所以∠ACB = 90°,因为△CAD∽△CEA,所以∠ADC = ∠CAE,因为$\overset{\frown}{AC}=\overset{\frown}{AC}$,所以∠ABC = ∠ADC,所以∠CAB = ∠ABC,因为∠ACB = 90°,所以∠ABC = 45°,所以∠ADC = 45°。
(1) 因为$\overset{\frown}{CD}=\overset{\frown}{DB}$,所以∠CAD = ∠DAB,因为DE = AD,所以∠DAB = ∠E,所以∠CAD = ∠E,又因为∠C = ∠C,所以△CAD∽△CEA。
(2) 连接BC,因为AB为直径,所以∠ACB = 90°,因为△CAD∽△CEA,所以∠ADC = ∠CAE,因为$\overset{\frown}{AC}=\overset{\frown}{AC}$,所以∠ABC = ∠ADC,所以∠CAB = ∠ABC,因为∠ACB = 90°,所以∠ABC = 45°,所以∠ADC = 45°。
8. (杭州中考)如图,锐角三角形 ABC 内接于⊙O,∠BAC 的平分线 AG 交⊙O 于点 G,交 BC 边于点 F,连接 BG.
(1)求证:△ABG∽△AFC;
(2)已知 AB = a,AC = AF = b,求线段 FG 的长(用含 a,b 的代数式表示);
(3)已知点 E 在线段 AF 上(不与点 A,点 F 重合),点 D 在线段 AE 上(不与点 A,点 E 重合),∠ABD = ∠CBE,求证:BG² = GE·GD.

(1)求证:△ABG∽△AFC;
(2)已知 AB = a,AC = AF = b,求线段 FG 的长(用含 a,b 的代数式表示);
(3)已知点 E 在线段 AF 上(不与点 A,点 F 重合),点 D 在线段 AE 上(不与点 A,点 E 重合),∠ABD = ∠CBE,求证:BG² = GE·GD.

答案:
(1) 因为AG平分∠BAC,所以∠BAG = ∠FAC,又因为∠G = ∠C,所以△ABG∽△AFC。
(2) 由
(1)知,△ABG∽△AFC,所以$\frac{AB}{AF}=\frac{AG}{AC}$,因为AC = AF = b,AB = AG = a,所以FG = AG - AF = a - b。
(3) 因为∠CAG = ∠CBG,∠BAG = ∠CAG,所以∠BAG = ∠CBG,因为∠ABD = ∠CBE,所以∠BAG + ∠ABD = ∠CBG + ∠CBE,即∠BDG = ∠EBG,又因为∠DGB = ∠BGE,所以△DGB∽△BGE,所以$\frac{GD}{BG}=\frac{BG}{GE}$,所以$BG^{2}=GE·GD$。
(1) 因为AG平分∠BAC,所以∠BAG = ∠FAC,又因为∠G = ∠C,所以△ABG∽△AFC。
(2) 由
(1)知,△ABG∽△AFC,所以$\frac{AB}{AF}=\frac{AG}{AC}$,因为AC = AF = b,AB = AG = a,所以FG = AG - AF = a - b。
(3) 因为∠CAG = ∠CBG,∠BAG = ∠CAG,所以∠BAG = ∠CBG,因为∠ABD = ∠CBE,所以∠BAG + ∠ABD = ∠CBG + ∠CBE,即∠BDG = ∠EBG,又因为∠DGB = ∠BGE,所以△DGB∽△BGE,所以$\frac{GD}{BG}=\frac{BG}{GE}$,所以$BG^{2}=GE·GD$。
查看更多完整答案,请扫码查看


