《2025年原创新课堂九年级数学下册人教版》

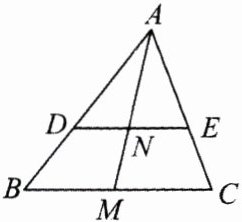
1. 如图，在△ABC中，DE//BC，$\frac{AD}{AB}=\frac{2}{3}$，M为BC上一点，AM交DE于点N.
（1）若AE = 4，求EC的长；
（2）若M为BC的中点，$S_{△ABC}=36$，求$S_{△ADN}$.

答案：
(1) 因为 $DE// BC$，所以 $\frac{AE}{AC}=\frac{AD}{AB}=\frac{2}{3}$，又因为 $AE = 4$，所以 $AC = 6$，则 $EC=6 - 4 = 2$。
(2) 因为 $M$ 为 $BC$ 的中点，$S_{\triangle ABM}=\frac{1}{2}S_{\triangle ABC}=18$，又因为 $DE// BC$，所以 $\triangle ADN\sim\triangle ABM$，则 $\frac{S_{\triangle ADN}}{S_{\triangle ABM}}=(\frac{AD}{AB})^2=\frac{4}{9}$，所以 $S_{\triangle ADN}=8$。

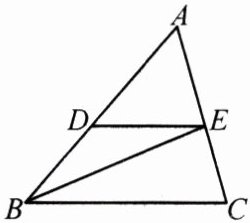
2. 如图，在△ABC中，BE平分∠ABC交AC于点E，过点E作ED//BC交AB于点D.
（1）求证：AE·BC = BD·AC；
（2）如果$S_{△ADE}=3$，$S_{△BDE}=2$，DE = 6，求BC的长.

答案：
(1) 因为 $BE$ 平分 $\angle ABC$，所以 $\angle ABE=\angle CBE$，又因为 $DE// BC$，所以 $\angle DEB=\angle CBE$，则 $\angle ABE=\angle DEB$，所以 $BD = DE$。因为 $DE// BC$，所以 $\triangle ADE\sim\triangle ABC$，所以 $\frac{AE}{AC}=\frac{DE}{BC}$，即 $\frac{AE}{AC}=\frac{BD}{BC}$，所以 $AE\cdot BC = BD\cdot AC$。
(2) 设 $\triangle ABE$ 中边 $AB$ 上的高为 $h$，则 $\frac{S_{\triangle ADE}}{S_{\triangle BDE}}=\frac{\frac{1}{2}AD\cdot h}{\frac{1}{2}BD\cdot h}=\frac{AD}{BD}=\frac{3}{2}$，因为 $\triangle ADE\sim\triangle ABC$，所以 $\frac{DE}{BC}=\frac{AD}{AB}$，即 $\frac{6}{BC}=\frac{3}{5}$，所以 $BC = 10$。

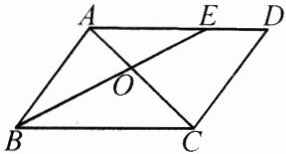
3. 如图，在□ABCD中，E是AD上的一点，已知AE∶ED = 2∶1，AO = 4，求OC的长.

答案： 因为四边形 $ABCD$ 为平行四边形，所以 $AD = BC$，$AD// BC$，所以 $\triangle AOE\sim\triangle COB$，则 $\frac{AO}{OC}=\frac{AE}{BC}$，又因为 $AE:ED = 2:1$，所以 $AE:AD = 2:3$，又因为 $AD = BC$，所以 $AE:BC = 2:3$，所以 $\frac{AO}{OC}=\frac{2}{3}$，又因为 $AO = 4$，所以 $OC = 6$。

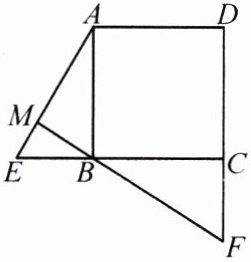
4. 如图，在正方形ABCD中，点E，F分别是边CB，DC延长线上的点，且BE = CF，连接AE，FB，FB的延长线交AE于点M. 求证：
（1）△BEM∽△BFC；
（2）$CF^{2}=FB·ME$.

答案： 证明：
(1) 因为四边形 $ABCD$ 是正方形，所以 $AB = BC$，$\angle ABC=\angle BCD = 90^{\circ}$，所以 $\angle ABE=\angle BCF = 90^{\circ}$，又因为 $BE = CF$，所以 $\triangle ABE\cong\triangle BCF(SAS)$，所以 $\angle E=\angle F$，又因为 $\angle EBM=\angle FBC$，所以 $\triangle BEM\sim\triangle BFC$。
(2) 由
(1)得 $\triangle BEM\sim\triangle BFC$，所以 $\frac{BE}{BF}=\frac{ME}{CF}$，因为 $BE = CF$，所以 $\frac{CF}{FB}=\frac{ME}{CF}$，即 $CF^{2}=FB\cdot ME$。