《2025年原创新课堂九年级数学下册人教版》

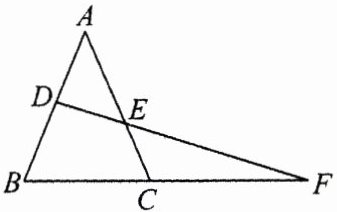
1.如图，在△ABC中，D为AB的中点，DF交AC于点E，交BC的延长线于点F.求证：AE·CF = BF·EC.

 

答案：
如图，过点C作CG//AB交DF于点G，因为△GCF∽△DBF，△GCE∽△DAE，所以$\frac{CF}{BF}=\frac{CG}{BD}$，$\frac{EC}{AE}=\frac{CG}{AD}$，因为D为AB的中点，所以AD = BD，所以$\frac{CF}{BF}=\frac{EC}{AE}$，所以AE·CF = BF·EC。

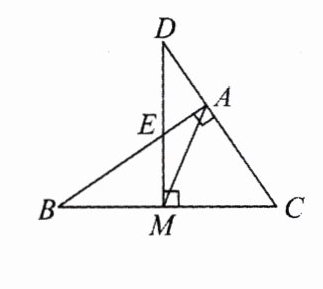
3.如图，在△ABC中，∠BAC = 90°.M为BC的中点，DM⊥BC交CA的延长线于点D，交AB于点E.求证：AM² = MD·ME.

答案： 因为∠BAC = 90°，M为BC的中点，所以AM = BM = CM，所以∠B = ∠BAM，因为∠B + ∠C = 90°，所以∠BAM + ∠C = 90°，因为∠C + ∠D = 90°，所以∠BAM = ∠D，因为∠AME = ∠DMA，所以△AME∽△DMA，所以$\frac{AM}{DM}=\frac{ME}{AM}$，所以AM² = MD·ME。

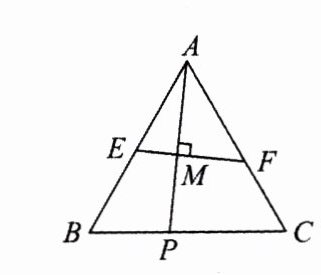
2.如图，点P是等边△ABC的一边BC上的任意一点，连接AP，M是AP的中点，过点M作AP的垂线交AB，AC于E，F两点，求证：$\frac{BP}{CF}=\frac{BE}{CP}$.

答案：
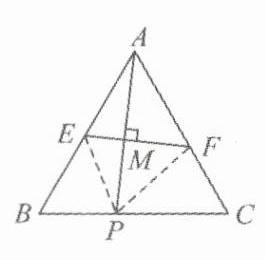
如图，连接PE，PF，因为△ABC为等边三角形，所以∠BAC = ∠B = ∠C = 60°，因为M是AP的中点，EF⊥AP，所以EF是线段AP的垂直平分线，所以EA = EP，FA = FP，在△EAF和△EPF中，$\begin{cases}EA = EP\\FA = FP\\EF = EF\end{cases}$，所以△EAF≌△EPF（SSS），所以∠EPF = ∠EAF = 60°，所以∠BPE + ∠CPF = 120°，又因为∠CFP + ∠CPF = 120°，所以∠BPE = ∠CFP，又因为∠B = ∠C，所以△BPE∽△CFP，所以$\frac{BP}{CF}=\frac{BE}{CP}$。

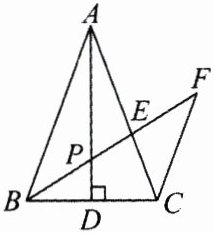
4.如图，在△ABC中，AB = AC，AD是垂线，点P在AD上，过点C作CF//AB，延长BP交AC于点E，交CF于点F.求证：BP² = PE·PF.

答案：
如图，连接PC，因为AB = AC，AD是中线，所以AD是BC的垂直平分线，所以PC = PB，所以∠PBC = ∠PCB，所以∠PCE = ∠ABP。因为CF//AB，所以∠PFC = ∠ABP，所以∠PCE = ∠PFC。又因为∠CPE = ∠FPC，所以△EPC∽△CPF，所以$\frac{PC}{PF}=\frac{PE}{PC}$，所以PC² = PE·PF。因为PC = BP，所以BP² = PE·PF。