《2025年原创新课堂九年级数学下册人教版》

9.（2024·滨州）点M（$x_1$，$y_1$）和点N（$x_2$，$y_2$）在反比例函数$y = \frac{k^2 - 2k + 3}{x}$（k为常数）的图象上，若$x_1 ＜ 0 ＜ x_2$，则$y_1$，$y_2$，0的大小关系为 （ ）
A.$y_1 ＜ y_2 ＜ 0$
B.$y_1 ＞ y_2 ＞ 0$
C.$y_1 ＜ 0 ＜ y_2$
D.$y_1 ＞ 0 ＞ y_2$

答案： C

10.（教材P9复习题8变式）在同一平面直角坐标系中，函数$y = kx + 1$（$k \neq 0$）和$y = \frac{k}{x}$（$k \neq 0$）的图象大致是 （ ）

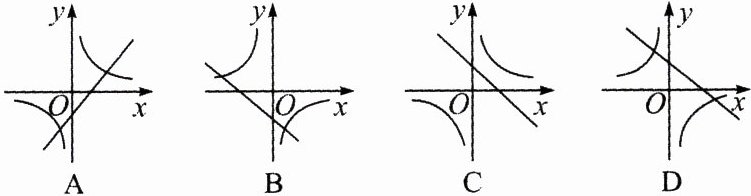
答案： D

11.（2024·陕西）已知点A（－2，$y_1$）和点B（m，$y_2$）均在反比例函数$y = - \frac{5}{x}$的图象上.若$0 ＜ m ＜ 1$，则$y_1 + y_2$______0.（填“＞”“＝”或“＜”）

答案： ＜

12.（2024·郑州校级月考）如图是三个反比例函数的图象的分支，其中$k_1$，$k_2$，$k_3$的大小关系是________________.

答案： $k_1 ＞ k_2 ＞ k_3$

13.已知反比例函数$y = \frac{2a + 3}{x}$，当$x = 3$时，$y = 2$.
（1）求a的值；
（2）当$1 ＜ x ＜ 3$时，求y的取值范围.

答案：
(1) 由题意得$2a + 3 = 6$，$\therefore a = \frac{3}{2}$
(2) $\because k = 6 ＞ 0$，$\therefore$在每个象限内，$y$随$x$的增大而减小，又$\because$当$x = 1$时，$y = 6$，当$x = 3$时，$y = 2$，$\therefore$当$1 ＜ x ＜ 3$时，$2 ＜ y ＜ 6$

14.平面直角坐标系中，A（$x_1$，$y_1$），B（$x_2$，$y_2$），C（$x_3$，$y_3$）是反比例函数$y = \frac{k}{x}$图象上的三点，且$x_1 + x_2 = 0$.
（1）若$x_1y_2 = - 2$，求k的值；
（2）若$x_1 = y_3$，求证：$x_3 + y_2 = 0$.

答案：
(1) $\because x_1 + x_2 = 0$，$\therefore x_1 = -x_2$. 又$\because x_1y_2 = -2$，$\therefore -x_2y_2 = -2$，$\therefore x_2y_2 = 2$，$\therefore k = 2$
(2) 由题意，可知$x_3y_3 = k$，$\therefore x_3 = \frac{k}{y_3}$，$\therefore x_3 + y_2 = \frac{k}{y_3} + y_2$. $\because x_1 = y_3$，$\therefore x_3 + y_2 = \frac{k}{y_1} + y_2 = y_1 + y_2$. 又$\because x_1 + x_2 = 0$，$\therefore \frac{k}{y_1} + \frac{k}{y_2} = \frac{k}{y_1y_2}(y_1 + y_2) = 0$. $\because k \neq 0$，$y_1y_2 \neq 0$，$\therefore y_1 + y_2 = 0$，$\therefore x_3 + y_2 = 0$

15.反比例函数$y = \frac{k}{x}$在第一象限的图象如图所示，过点A（1，0）作x轴的垂线，交反比例函数$y = \frac{k}{x}$的图象于点M，$\triangle AOM$的面积为3.
（1）求反比例函数的解析式；
（2）设点B的坐标为（t，0），其中$t ＞ 1$，若以AB为一边的正方形有一个顶点在反比例函数$y = \frac{k}{x}$的图象上，请直接写出t的值.

答案：
(1) $\because$点$A(1, 0)$，$\triangle AOM$的面积为3，$\therefore OA = 1$，$\frac{1}{2}OA \cdot AM = 3$，$\therefore AM = 6$，$\therefore M(1, 6)$. 将$M(1, 6)$代入反比例函数解析式，得$k = 6$，$\therefore$反比例函数的解析式$y = \frac{6}{x}$
(2) $t = 3$或7