《2025年原创新课堂九年级数学下册人教版》

12.已知$\frac{a}{4}=\frac{b}{3}$,则$\frac{a - b}{b}$的值是 （ ）
A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.3
D.$\frac{1}{3}$

答案： D

13.(2024·连云港)下列网格中各个小正方形的边长均为 1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为 （ ）

A.甲和乙
B.乙和丁
C.甲和丙
D.甲和丁

答案： D

14.(教材 P28 习题 8 变式)如图,一般书本的纸张是由原纸张多次对开得到,矩形 ABCD 沿EF 对开后,再把矩形 EFCD 沿 MN 对开,依此类推.若各种开本的矩形都相似,那么$\frac{AB}{AD}$等于 （ ）

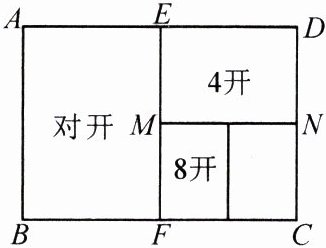
A.0.618
B.$\frac{\sqrt{2}}{2}$
C.$\sqrt{2}$
D.2

答案： B

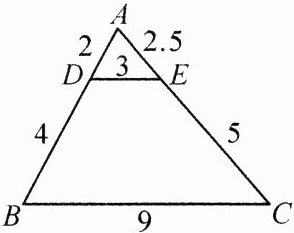
15.如图,DE//BC.
(1)求$\frac{AD}{AB},\frac{AE}{AC},\frac{DE}{BC}$的值;
(2)求证:△ADE∽△ABC.

答案：
(1) 因为$DE// BC$，所以$\frac{AD}{AB}=\frac{AE}{AC}$，因为$AD = 2$，$DB = 4$，$AE = 2.5$，$CE = 5$，所以$AB=AD + BD = 6$，$AC=AE + CE = 7.5$，所以$\frac{AD}{AB}=\frac{1}{3}$，$\frac{AE}{AC}=\frac{1}{3}$，因为$DE = 3$，$BC = 9$，所以$\frac{DE}{BC}=\frac{1}{3}$
(2) 因为$DE// BC$，所以$\angle ADE=\angle D$，$\angle AED=\angle C$，又因为$\angle DAE=\angle BAC$，$\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}=\frac{1}{3}$，所以$\triangle ADE\sim\triangle ABC$

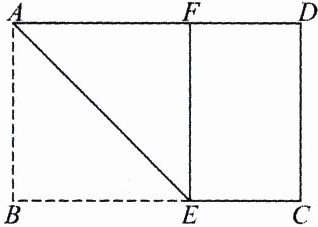
16.如图,在矩形 ABCD 中,AB = 1,在 BC 上取一点 E,沿 AE 将△ABE 向上折叠,使点 B落在 AD 上的点 F 处,若四边形 EFDC 与矩形 ABCD 相似,求 AD 的长.

答案： 由题意易知四边形$ABEF$为正方形，设$AD = x$，因为$AB = 1$，所以$FD=x - 1$，$FE = 1$，因为四边形$EFDC$与矩形$ABCD$相似，所以$\frac{FE}{FD}=\frac{AD}{AB}$，即$\frac{1}{x - 1}=\frac{x}{1}$，整理得$x^{2}-x - 1 = 0$，解得$x_1=\frac{\sqrt{5}+1}{2}$，$x_2=\frac{1 - \sqrt{5}}{2}$（不合题意，舍去），经检验，$x_1=\frac{\sqrt{5}+1}{2}$是原方程的解，所以$AD=\frac{\sqrt{5}+1}{2}$

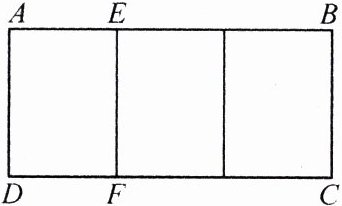
17.(2024·郑州管城区月考)如图,把一个矩形ABCD 划分成三个全等的小矩形.
(1)若原矩形 ABCD 的长 AB = 6,宽 BC = 4.问:每个小矩形与原矩形相似吗? 请说明理由;
(2)若原矩形的长 AB = a,宽 BC = b,且每个小矩形与原矩形相似,求原矩形长 a 与宽b 应满足的关系式.

答案：
(1) 不相似。理由如下：因为原矩形$ABCD$的长$AB = 6$，宽$BC = 4$，所以划分后小矩形的长为$AD = 4$，宽为$AE = 6\div3 = 2$，又因为$\frac{AB}{BC}=\frac{6}{4}\neq\frac{4}{2}=\frac{AD}{AE}$，即原矩形与每个小矩形的边不成比例，所以每个小矩形与原矩形不相似
(2) 因为原矩形的长$AB = a$，宽$BC = b$，所以划分后小矩形的长为$AD = b$，宽为$AE=\frac{a}{3}$，又因为每个小矩形与原矩形相似，所以$\frac{AB}{BC}=\frac{AD}{AE}$，所以$\frac{a}{b}=\frac{b}{\frac{a}{3}}$，即$a^{2}=3b^{2}$