《2025年原创新课堂九年级数学下册人教版》

1.(2024·牡丹江)如图，某数学活动小组用高度为1.5米的测角仪BC，对垂直于地面CD的建筑物AD的高度进行测量，BC⊥CD于点C.在B处测得A的仰角∠ABE = 45°，然后将测角仪向建筑物方向水平移动6米至FG处，FG⊥CD于点G，测得A的仰角∠AFE = 58°，BF的延长线交AD于点E，求建筑物AD的高度.(结果保留小数点后一位，参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60)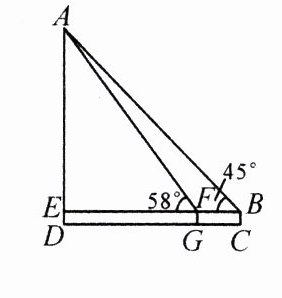

答案： 根据题意可知四边形BEDC是矩形，所以DE = BC = 1.5 m。因为∠ABE = 45°，∠AFE = 58°。 由于$\tan\angle ABE=\frac{AE}{BE}$，$\tan\angle AFE=\frac{AE}{EF}$，所以AE = BE·$\tan45^{\circ}$= BE，EF = $\frac{AE}{\tan58^{\circ}}$。又因为BE = EF + BF，所以AE = 6 + $\frac{AE}{\tan58^{\circ}}$，进而得出AE≈16。所以AD = AE + DE = 17.5(米)，答：建筑物AD的高度约为17.5米。

2.(2024·宜宾)宜宾地标广场位于三江汇合口(如图1，左侧是岷江，右侧是金沙江，正面是长江).某同学在数学实践中测量长江口的宽度，他在长江口的两岸选择两个标点C，D，在地标广场上选择两个观测点A，B(点A，B，C，D在同一水平面，且AB//CD).如图2所示，在点A处测得点C在北偏西18.17°方向上，测得点D在北偏东21.34°方向上；在B处测得点C在北偏西21.34°方向上，测得点D在北偏东18.17°方向上，测得AB = 100米.求长江口的宽度CD的值.(结果精确到1米.参考数据：sin18.17°≈0.31，cos18.17°≈0.95，tan18.17°≈0.33，sin21.34°≈0.36，cos21.34°≈0.93，tan21.34°≈0.39)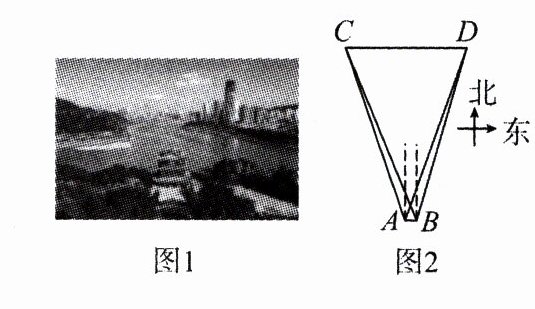

答案： 过点A作AE⊥CD，垂足为E，过点B作BF⊥CD，垂足为F，因为AB//CD，所以AE = BF。由题意得AB = EF = 100 m，设AE = BF = x m，在Rt△ACE中，∠CAE = 18.17°，所以CE = AE·$\tan18.17^{\circ}$≈0.33x(m)，在Rt△BDF中，∠DBF = 18.17°，所以DF = BF·$\tan18.17^{\circ}$≈0.33x(m)，在Rt△AED中，∠EAD = 21.34°，所以DE = AE·$\tan21.34^{\circ}$≈0.39x(m)，因为DE = EF + DF，所以0.39x = 100 + 0.33x，解得x = $\frac{5000}{3}$，所以CD = CE + DE = 0.33x + 0.39x = 0.72x = 1200(m)，答：长江口的宽度CD的值约为1200 m。

3.(2024·天津)综合与实践活动中，要用测角仪测量天津海河上一座桥的桥塔AB的高度(如图1).某学习小组设计了一个方案：如图2，点C，D，E依次在同一条水平直线上，DE = 36 m，EC⊥AB，垂足为C.在D处测得桥塔顶部B的仰角(∠CDB)为45°，测得桥塔底部A的俯角(∠CDA)为6°，又在E处测得桥塔顶部B的仰角(∠CEB)为31°.
(1)求线段CD的长(结果取整数)；
(2)求桥塔AB的高度(结果取整数).
参考数据：tan31°≈0.6，tan6°≈0.1.

答案：
(1)设CD = x，因为DE = 36 m，所以CE = CD + DE = (x + 36)m，因为EC⊥AB，所以∠BCE = ∠ACD = 90°，因为∠CDB = 45°，所以BC = CD = x m。因为$\tan\angle CEB=\frac{BC}{CE}$，∠CEB = 31°，所以BC = CE·$\tan\angle CEB$=(x + 36)·$\tan31^{\circ}$，所以x = (x + 36)·$\tan31^{\circ}$，解得x = 54。答：线段CD的长约为54 m。
(2)因为$\tan\angle CDA=\frac{AC}{CD}$，∠CDA = 6°，所以AC = CD·$\tan\angle CDA$≈54×$\tan6^{\circ}$≈54×0.1 = 5.4(m)。所以AB = AC + BC≈5.4 + 54≈59(m)。答：桥塔AB的高度约为59m。