《2025年原创新课堂九年级数学下册人教版》

1.（河池中考）在Rt△ABC中，∠C = 90°，BC = 5，AC = 12，则sinB的值是 （ ）
A.$\frac{5}{12}$
B.$\frac{12}{5}$
C.$\frac{5}{13}$
D.$\frac{12}{13}$

答案： D

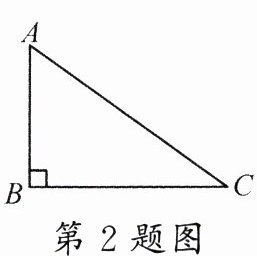
2.（2024·安阳滑县期末）如图，在Rt△ABC中，∠ABC = 90°，AB = 3，BC = 4，则sinA的值是 （ ）

A.$\frac{4}{3}$
B.$\frac{3}{4}$
C.$\frac{3}{5}$
D.$\frac{4}{5}$

答案： D

3.在直角三角形ABC中，若各边的长都扩大到原来的5倍，则∠A的正弦值 （ ）
A.扩大到原来的5倍
B.缩小到原来的$\frac{1}{5}$
C.不变
D.不能确定

答案： C

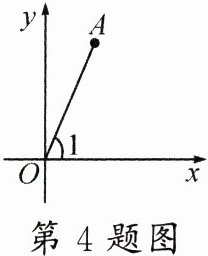
4.（龙岩中考）如图，若点A的坐标为（1,$\sqrt{3}$），则sin∠1 = ________.

答案： $\frac{\sqrt{3}}{2}$

5.在Rt△ABC中，∠ACB = 90°，CD是斜边AB上的中线，CD = 4，AC = 6，则sinB的值是______.

答案： $\frac{3}{4}$

6.分别求出图中∠A，∠B的正弦值.

答案： 如图①，由勾股定理，得$AC = \sqrt{6^{2}-2^{2}} = 4\sqrt{2}$，$\sin A=\frac{BC}{AB}=\frac{1}{3}$，$\sin B=\frac{AC}{AB}=\frac{2\sqrt{2}}{3}$；如图②，由勾股定理，得$AB = \sqrt{AC^{2}+BC^{2}} = \sqrt{36 + 4} = 2\sqrt{10}$，$\sin A=\frac{BC}{AB}=\frac{2}{2\sqrt{10}}=\frac{\sqrt{10}}{10}$，$\sin B=\frac{AC}{AB}=\frac{6}{2\sqrt{10}}=\frac{3\sqrt{10}}{10}$

7.如图，⊙O的半径为3，弦AB的长为4.求sinA的值.

答案： 过点$O$作$OC\perp AB$于点$C$，则有$AC = BC$，$\because AB = 4$，$\therefore AC = 2$，在$Rt\triangle AOC$中，$OC = \sqrt{OA^{2}-AC^{2}} = \sqrt{3^{2}-2^{2}} = \sqrt{5}$，$\therefore \sin A=\frac{OC}{OA}=\frac{\sqrt{5}}{3}$

8.（云南中考）在△ABC中，∠ABC = 90°.若AC = 100，sinA = $\frac{3}{5}$，则AB的长是 （ ）
A.$\frac{500}{3}$
B.$\frac{503}{5}$
C.60
D.80

答案： D

9.如图，在△ABC中，∠C = 90°，sinA = $\frac{1}{4}$，BC = 2，求AC，AB的长.

答案： $\because \sin A=\frac{1}{4}$，$\therefore \frac{BC}{AB}=\frac{1}{4}$，又$\because BC = 2$，$\therefore AB = 4BC = 4\times2 = 8$，在$Rt\triangle ABC$中，由勾股定理得$AC = \sqrt{AB^{2}-BC^{2}} = \sqrt{8^{2}-2^{2}} = 2\sqrt{15}$

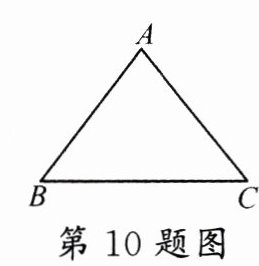
10.（2024·临夏州）如图，在△ABC中，AB = AC = 5，sinB = $\frac{4}{5}$，则BC的长是 （ ）


A.3
B.6
C.8
D.9

答案： B