《2025年原创新课堂九年级数学下册人教版》

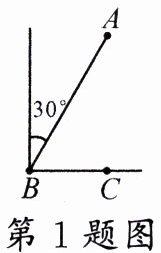
1.(2024·广州)如图，海中有一小岛A，在B点测得小岛A在北偏东30°方向上，渔船从B点出发由西向东航行10 n mile到达C点，在C点测得小岛A恰好在正北方向上，此时渔船与小岛A的距离为 （ ）

A.$\frac{10\sqrt{3}}{3}$ n mile
B.$\frac{20\sqrt{3}}{3}$ n mile
C.20 n mile
D.10$\sqrt{3}$ n mile

答案： D

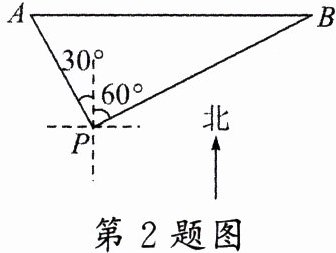
2.丹丹在汨罗江国际龙舟竞渡中心广场点P处观看200米直道竞速赛.如图所示，赛道AB为东西方向，赛道起点A位于点P的北偏西30°方向上，终点B位于点P的北偏东60°方向上，AB = 200米，则点P到赛道AB的距离约为______米（结果保留整数，参考数据：$\sqrt{3}$≈1.732）.

答案： 87

3.(2024·甘孜州)如图，一艘海轮位于灯塔P的北偏东37°方向，距离灯塔100海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处.这时，B处距离A处有多远?（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）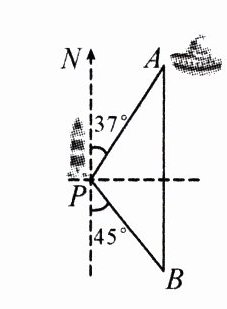

答案： 过P作PC⊥AB于C，在Rt△APC中，因为∠A = 37°，AP = 100海里，所以PC = AP·sinA = 100×sin37°≈100×0.6 = 60（海里），AC = AP·cos37°≈100×0.8 = 80（海里），在Rt△PBC中，因为∠B = 45°，所以BC = PC = 60（海里），所以AB = AC + BC = 80 + 60 = 140（海里），答：B处距离A处约有140海里

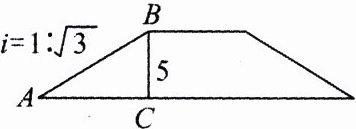
4.如图，某地修建的一座建筑物的截面图的高BC = 5 m，坡面AB的坡度为1∶$\sqrt{3}$，则AB的长度为 （ ）

A.10 m
B.10$\sqrt{3}$ m
C.5 m
D.5$\sqrt{3}$ m

答案： A

5.(2024·深圳)爬坡时坡面与水平面夹角为α，则每爬1 m耗能(1.025 - cosα)J，若某人爬了1000 m，该坡角为30°，则他耗能 （ ）（参考数据：$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414）
A.58 J
B.159 J
C.1025 J
D.1732 J

答案： B

6.(2024·湖北)为了防洪需要，某地决定新建一座拦水坝，如图，拦水坝的横断面为梯形ABCD，斜面坡度i = 3∶4是指坡面的铅直高度AF与水平宽度BF的比.已知斜坡CD长度为20米，∠C = 18°，求斜坡AB的长.（结果精确到0.1米.参考数据：sin18°≈0.31，cos18°≈0.95，tan18°≈0.32）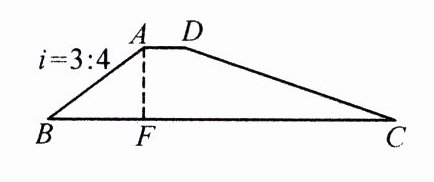

答案： 过点D作DE⊥BC，垂足为E，由题意得AF⊥BC，DE = AF，因为斜面AB的坡度i = 3 : 4，所以$\frac{AF}{BF}=\frac{3}{4}$，设AF = 3x米，则BF = 4x米，在Rt△ABF中，AB = $\sqrt{AF^{2}+BF^{2}}=\sqrt{(3x)^{2}+(4x)^{2}} = 5x$（米），在Rt△DEC中，因为∠C = 18°，CD = 20米，所以DE = CD·sin18°≈20×0.31 = 6.2（米），所以AF = DE = 6.2米，所以3x = 6.2，解得x = $\frac{31}{15}$，所以AB = 5x≈10.3（米），所以斜坡AB的长约为10.3米