11.(齐齐哈尔中考)在$\triangle ABC$中,$AB = 3\sqrt{6}$,$AC = 6$,$\angle B = 45^{\circ}$,则$BC =$________________.
答案:
$3\sqrt{3}+3$或$3\sqrt{3}-3$
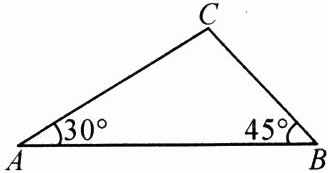
12. 如图,在$\triangle ABC$中,$\angle A = 30^{\circ}$,$\angle B = 45^{\circ}$,$AC = 2\sqrt{3}$,求$AB$的长.

答案:
过点$C$作$CD\perp AB$于点$D$,$\therefore\angle ADC=\angle BDC = 90^{\circ}$,
因为$\angle B = 45^{\circ}$,$\therefore\angle BCD=\angle B = 45^{\circ}$,$\therefore CD = BD$,因为$\angle A = 30^{\circ}$,$AC = 2\sqrt{3}$,$\therefore CD=\sqrt{3}$,$\therefore BD = CD=\sqrt{3}$,由勾股定理得$AD=\sqrt{AC^{2}-CD^{2}} = 3$,$\therefore AB=AD + BD=3+\sqrt{3}$
13.(2024·浙江)如图,在$\triangle ABC$中,$AD\perp BC$,$AE$是$BC$边上的中线,$AB = 10$,$AD = 6$,$\tan\angle ACB = 1$.
(1)求$BC$的长;
(2)求$\sin\angle DAE$的值.

(1)求$BC$的长;
(2)求$\sin\angle DAE$的值.

答案:
(1) 因为$AD\perp BC$,$AB = 10$,$AD = 6$,$\therefore BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{10^{2}-6^{2}} = 8$;因为$\tan\angle ACB = 1$,$\therefore CD = AD = 6$,$\therefore BC=BD + CD=8 + 6 = 14$
(2) 因为$AE$是$BC$边上的中线,$\therefore CE=\frac{1}{2}BC = 7$,$\therefore DE=CE - CD=7 - 6 = 1$,因为$AD\perp BC$,$\therefore AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{6^{2}+1^{2}}=\sqrt{37}$,$\therefore\sin\angle DAE=\frac{DE}{AE}=\frac{1}{\sqrt{37}}=\frac{\sqrt{37}}{37}$
(1) 因为$AD\perp BC$,$AB = 10$,$AD = 6$,$\therefore BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{10^{2}-6^{2}} = 8$;因为$\tan\angle ACB = 1$,$\therefore CD = AD = 6$,$\therefore BC=BD + CD=8 + 6 = 14$
(2) 因为$AE$是$BC$边上的中线,$\therefore CE=\frac{1}{2}BC = 7$,$\therefore DE=CE - CD=7 - 6 = 1$,因为$AD\perp BC$,$\therefore AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{6^{2}+1^{2}}=\sqrt{37}$,$\therefore\sin\angle DAE=\frac{DE}{AE}=\frac{1}{\sqrt{37}}=\frac{\sqrt{37}}{37}$
14. 知识再现:如图1,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle A$,$\angle B$,$\angle C$的对边分别为$a$,$b$,$c$.
$\because\sin A = \frac{a}{c}$,$\sin B = \frac{b}{c}$,$\therefore c = \frac{a}{\sin A}$,$c = \frac{b}{\sin B}$.
$\therefore\frac{a}{\sin A} = \frac{b}{\sin B}$.
(1)拓展探究:如图2,在锐角三角形$ABC$中,$\angle A$,$\angle B$,$\angle C$的对边分别为$a$,$b$,$c$.请探究$\frac{a}{\sin A}$,$\frac{b}{\sin B}$,$\frac{c}{\sin C}$之间的关系,并写出探究过程;
(2)解决问题:如图3,为测量点$A$到河对岸点$B$的距离,选取与点$A$在河岸同一侧的点$C$,测得$AC = 60$m,$\angle A = 75^{\circ}$,$\angle C = 60^{\circ}$.请用探究探究中的结论,求点$A$到点$B$的距离.

$\because\sin A = \frac{a}{c}$,$\sin B = \frac{b}{c}$,$\therefore c = \frac{a}{\sin A}$,$c = \frac{b}{\sin B}$.
$\therefore\frac{a}{\sin A} = \frac{b}{\sin B}$.
(1)拓展探究:如图2,在锐角三角形$ABC$中,$\angle A$,$\angle B$,$\angle C$的对边分别为$a$,$b$,$c$.请探究$\frac{a}{\sin A}$,$\frac{b}{\sin B}$,$\frac{c}{\sin C}$之间的关系,并写出探究过程;
(2)解决问题:如图3,为测量点$A$到河对岸点$B$的距离,选取与点$A$在河岸同一侧的点$C$,测得$AC = 60$m,$\angle A = 75^{\circ}$,$\angle C = 60^{\circ}$.请用探究探究中的结论,求点$A$到点$B$的距离.

答案:
(1) 如图,作$CD\perp AB$于点$D$,$AE\perp BC$于点$E$,在$Rt\triangle ABE$中,$\sin B=\frac{AE}{AB}=\frac{AE}{c}$,同理:$\sin B=\frac{CD}{BC}=\frac{CD}{a}$,$\sin\angle BAC=\frac{CD}{AC}=\frac{CD}{b}$,$\sin\angle BCA=\frac{AE}{AC}=\frac{AE}{b}$,$\therefore AE = c\sin B$,$AE = b\sin\angle BCA$,$CD = a\sin B$,$CD = b\sin\angle BAC$,$\therefore\frac{b}{\sin B}=\frac{c}{\sin\angle BCA}$,$\frac{a}{\sin\angle BAC}=\frac{b}{\sin B}$,$\therefore\frac{a}{\sin\angle BAC}=\frac{b}{\sin B}=\frac{c}{\sin\angle BCA}$
(2) 在$\triangle ABC$中,$\angle CBA=180^{\circ}-\angle A-\angle C=180^{\circ}-75^{\circ}-60^{\circ}=45^{\circ}$,因为$\frac{AB}{\sin C}=\frac{AC}{\sin\angle CBA}$,$\therefore\frac{AB}{\sin60^{\circ}}=\frac{60}{\sin45^{\circ}}$,$\therefore AB = 30\sqrt{6}$,$\therefore$点$A$到点$B$的距离为$30\sqrt{6}\text{ m}$ (注:文档中实际图片编号需根据实际情况确定,这里假设为1)
(注:文档中实际图片编号需根据实际情况确定,这里假设为1)
(1) 如图,作$CD\perp AB$于点$D$,$AE\perp BC$于点$E$,在$Rt\triangle ABE$中,$\sin B=\frac{AE}{AB}=\frac{AE}{c}$,同理:$\sin B=\frac{CD}{BC}=\frac{CD}{a}$,$\sin\angle BAC=\frac{CD}{AC}=\frac{CD}{b}$,$\sin\angle BCA=\frac{AE}{AC}=\frac{AE}{b}$,$\therefore AE = c\sin B$,$AE = b\sin\angle BCA$,$CD = a\sin B$,$CD = b\sin\angle BAC$,$\therefore\frac{b}{\sin B}=\frac{c}{\sin\angle BCA}$,$\frac{a}{\sin\angle BAC}=\frac{b}{\sin B}$,$\therefore\frac{a}{\sin\angle BAC}=\frac{b}{\sin B}=\frac{c}{\sin\angle BCA}$
(2) 在$\triangle ABC$中,$\angle CBA=180^{\circ}-\angle A-\angle C=180^{\circ}-75^{\circ}-60^{\circ}=45^{\circ}$,因为$\frac{AB}{\sin C}=\frac{AC}{\sin\angle CBA}$,$\therefore\frac{AB}{\sin60^{\circ}}=\frac{60}{\sin45^{\circ}}$,$\therefore AB = 30\sqrt{6}$,$\therefore$点$A$到点$B$的距离为$30\sqrt{6}\text{ m}$
 (注:文档中实际图片编号需根据实际情况确定,这里假设为1)
(注:文档中实际图片编号需根据实际情况确定,这里假设为1) 查看更多完整答案,请扫码查看


