《2025年原创新课堂九年级数学下册人教版》

10.（2024·河南）如图，在$\square ABCD$中，对角线$AC$，$BD$相交于点$O$，点$E$为$OC$的中点，$EF // AB$交$BC$于点$F$.若$AB = 4$，则$EF$的长为 （ ）

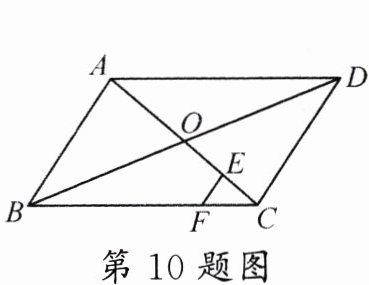
A. $\frac{1}{2}$
B. 1
C. $\frac{4}{3}$
D. 2

答案： B

11. 如图，在矩形$ABCD$中，若$AB = 3$，$AC = 5$，$\frac{AF}{FC}=\frac{1}{4}$，则$AE$的长为____.

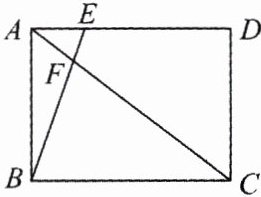
答案： 1

12. 如图，$\square ABCD$中，过点$B$作直线$BF$分别交$AC$，$AD$于点$O$，$E$，交$CD$的延长线于点$F$.
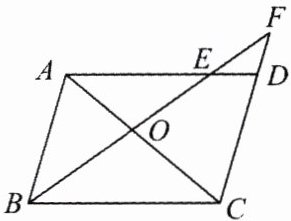
（1）若$OE = 2$，$BE = 5$，求$\frac{OA}{OC}$的值；
（2）求证：$OB^{2}=OE\cdot OF$.

答案：
(1) 因为$OE = 2$，$BE = 5$，所以$OB = BE - OE = 3$。因为四边形$ABCD$是平行四边形，所以$AD// BC$，所以$\triangle AOE\sim\triangle COB$，所以$\frac{OA}{OC}=\frac{OE}{OB}=\frac{2}{3}$
(2) 因为四边形$ABCD$是平行四边形，所以$AB// CD$，所以$\triangle AOB\sim\triangle COF$，所以$\frac{OA}{OC}=\frac{OB}{OF}$，又因为$\frac{OA}{OC}=\frac{OE}{OB}$，所以$\frac{OB}{OF}=\frac{OE}{OB}$，$OB^{2}=OE\cdot OF$

13. 阅读下面材料：
小波遇到这样一个问题：如图1，在$\triangle ABC$中，$BE$是$AC$边上的中线，点$D$在$BC$边上，$AD$与$BE$相交于点$P$.
（1）小波发现，$\frac{DB}{BC}=\frac{2}{3}$，过点$C$作$CF // AD$交$BE$的延长线于点$F$，通过构造$\triangle CEF$（如图2），经过推理和计算得到$\frac{AP}{PD}$的值为________；
（2）参考小波思考问题的方法，解决问题：
①如图3，在$\triangle ABC$中，点$D$在$BC$的延长线上，$\frac{DB}{BC}=\frac{4}{3}$，点$E$在$AC$上，且$\frac{AE}{EC}=\frac{3}{2}$，求$\frac{AP}{PD}$的值；
②如图4，在$\triangle ABC$中，点$D$在$BC$的延长线上，$\frac{DB}{BC}=\frac{4}{3}$，点$E$在$AC$的延长线上，且$\frac{AE}{EC}=\frac{7}{2}$，求$\frac{AP}{PD}$的值.

答案： $\frac{3}{2}$@@①如图3，过$A$作$AF// BC$，交$BP$延长线于点$F$，所以$\triangle AFE\sim\triangle CBE$，所以$\frac{AF}{BC}=\frac{AE}{EC}$，因为$\frac{AE}{EC}=\frac{3}{2}$，所以$\frac{AF}{BC}=\frac{3}{2}$，设$AF = 3x$，$BC = 2x$，因为$\frac{DB}{BC}=\frac{4}{3}$，所以$BD=\frac{8}{3}x$，因为$AF// BD$，所以$\triangle AFP\sim\triangle DBP$，所以$\frac{AP}{PD}=\frac{AF}{BD}=\frac{9}{8}$ ②如图4，过$C$作$CF// AP$交$PB$于$F$，所以$\triangle BCF\sim\triangle BDP$，所以$\frac{BC}{BD}=\frac{CF}{PD}=\frac{3}{4}$，设$CF = 3x$，$PD = 4x$，因为$CF// AP$，所以$\triangle ECF\sim\triangle EAP$，所以$\frac{EC}{AE}=\frac{CF}{AP}=\frac{2}{7}$，所以$AP=\frac{21}{2}x$，所以$\frac{AP}{DP}=\frac{\frac{21x}{2}}{4x}=\frac{21}{8}$，所以$\frac{AP}{PD}$的值为$\frac{21}{8}$