《2025年原创新课堂九年级数学下册人教版》

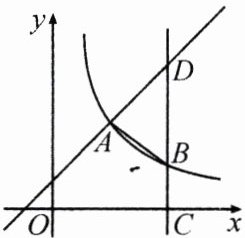
1.(2024·兰州)如图，反比例函数$y = \frac{k}{x}(x＞0)$与一次函数$y = mx + 1$的图象交于点$A(2,3)$，点$B$是反比例函数图象上一点，$BC\perp x$轴于点$C$，交一次函数的图象于点$D$，连接$AB$.
(1)求反比例函数$y = \frac{k}{x}$与一次函数$y = mx + 1$的解析式；
(2)当$OC = 4$时，求$\triangle ABD$的面积.

答案：
(1) 因为反比例函数$y = \frac{k}{x}(x＞0)$与一次函数$y = mx + 1$的图象交于点$A(2,3)$，所以$k = 2×3 = 6$，$3 = 2m + 1$，解得$k = 6$，$m = 1$，所以一次函数解析式为$y = x + 1$，反比例函数解析式为$y = \frac{6}{x}$。
(2) 将$x = 4$代入一次函数得$y = 5$，所以$D(4,5)$，将$x = 4$代入反比例函数得$y = \frac{3}{2}$，所以$B(4,\frac{3}{2})$，所以$BD = 5 - \frac{3}{2} = \frac{7}{2}$，所以$S_{\triangle ABD} = \frac{1}{2}×\frac{7}{2}×(4 - 2) = \frac{7}{2}$。

2.(2024·连云港)如图1，在平面直角坐标系$xOy$中，一次函数$y = kx + 1(k\neq0)$的图象与反比例函数$y = \frac{6}{x}$的图象交于点$A$，$B$，与$y$轴交于点$C$，点$A$的横坐标为$2$.
(1)求$k$的值；
(2)利用图象直接写出$kx + 1＜\frac{6}{x}$时$x$的取值范围；
(3)如图2，将直线$AB$沿$y$轴向下平移$4$个单位，与函数$y = \frac{6}{x}(x＞0)$的图象交于点$D$，与$y$轴交于点$E$，再将函数$y = \frac{6}{x}(x＞0)$的图象沿$AB$平移，使点$A$，$D$分别平移到点$C$，$F$处，求图中阴影部分的面积.

答案：
(1) 因为点$A$在$y = \frac{6}{x}$的图象上，所以当$x = 2$时，$y = \frac{6}{2} = 3$，所以$A(2,3)$，将点$A(2,3)$代入$y = kx + 1$，得$k = 1$。
(2) 由
(1)可知一次函数解析式为$y = x + 1$，联立方程组$\begin{cases}y = \frac{6}{x}\\y = x + 1\end{cases}$，解得$\begin{cases}x = 2\\y = 3\end{cases}$，$\begin{cases}x = - 3\\y = - 2\end{cases}$，所以$A(2,3)$，$B(-3,-2)$，根据图象可知$kx + 1 ＜ \frac{6}{x}$的解集为$x ＜ - 3$或$0 ＜ x ＜ 2$。
(3) 由题意可知$C(0,1)$，$CE = 4$，过点$C$作$CG\perp DE$，垂足为$G$，因为$CE = 4$，$\angle CEG = 45^{\circ}$，所以$CG = 2\sqrt{2}$，又因为$A(2,3)$，$C(0,1)$，所以$AC = 2\sqrt{2}$，由平移性质可知，阴影部分面积就是$\square ACFD$的面积，即$2\sqrt{2}×2\sqrt{2} = 8$。

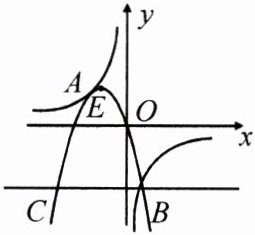
3.抛物线$y = ax^{2}+bx + c(a＜0)$与双曲线$y = \frac{k}{x}$相交于点$A$，$B$，且抛物线经过坐标原点，点$A$的坐标为$(-2,2)$，点$B$在第四象限内，过点$B$作直线$BC// x$轴，点$C$为直线与抛物线的另一交点，已知直线$BC$与$x$轴之间的距离是点$B$到$y$轴的距离的$4$倍.记抛物线顶点为$E$.
(1)求双曲线和抛物线的解析式；
(2)计算$\triangle ABC$与$\triangle ABE$的面积.

答案：
(1) 由点$A(-2,2)$在双曲线上得双曲线的解析式为$y = - \frac{4}{x}$，设点$B$的坐标为$(m,-4m)$且$m＞0$，代入$y = - \frac{4}{x}$，得$m = 1$，所以$B(1,-4)$，由题意知$c = 0$，把$A$，$B$的坐标代入$y = ax^{2}+bx$，得$\begin{cases}4a - 2b = 2\\a + b = - 4\end{cases}$，解得$\begin{cases}a = - 1\\b = - 3\end{cases}$，所以$y = - x^{2}-3x$。
(2) 因为抛物线的解析式为$y = - x^{2}-3x = -(x + \frac{3}{2})^{2}+\frac{9}{4}$，所以抛物线的顶点是$E(-\frac{3}{2},\frac{9}{4})$，对称轴是直线$x = - \frac{3}{2}$，因为$B(1,-4)$，由抛物线的对称性得$C(-4,-4)$，所以$S_{\triangle ABC} = \frac{1}{2}×5×6 = 15$，由$A$，$B$两点坐标分别为$(-2,2)$，$(1,-4)$可求得直线$AB$的解析式为$y = - 2x - 2$，设抛物线的对称轴交$AB$于点$F$，求得$F(-\frac{3}{2},1)$，$EF = \frac{9}{4}-1 = \frac{5}{4}$，所以$S_{\triangle ABE} = S_{\triangle AEF}+S_{\triangle BEF} = \frac{1}{2}×\frac{5}{4}×\frac{1}{2}+\frac{1}{2}×\frac{5}{4}×\frac{5}{2}=\frac{15}{8}$。