11.(连云港中考)如图,在6×6正方形网格中,△ABC的顶点A,B,C都在网格线上,且都是小正方形边的中点,则sinA = ________.
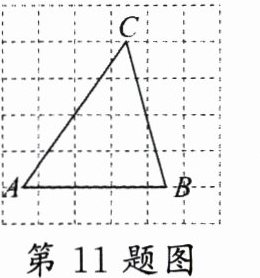

答案:
$\frac{4}{5}$
12.(常州中考)如图,在四边形ABCD中,∠A = ∠ABC = 90°,DB平分∠ADC.若AD = 1,CD = 3,则sin∠ABD = ________.
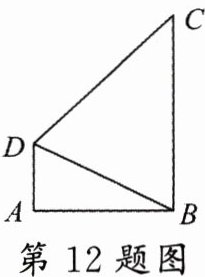

答案:
$\frac{\sqrt{6}}{6}$
13.如图,在△ABC中,∠A = 120°,AB = 4,AC = 2,求sinB的值.


答案:
作$CD\perp BA$的延长线于点$D$,$\therefore \angle ADC = 90^{\circ}$,$\because \angle BAC = 120^{\circ}$,$\therefore \angle DAC = 180^{\circ}-\angle BAC = 60^{\circ}$,$\therefore \angle ACD = 30^{\circ}$,$\because AC = 2$,$\therefore AD = 1$,$CD = \sqrt{3}$,$\therefore BD = 5$,在$Rt\triangle BCD$中,$BC = \sqrt{BD^{2}+CD^{2}} = 2\sqrt{7}$,$\therefore \sin B=\frac{CD}{BC}=\frac{\sqrt{3}}{2\sqrt{7}}=\frac{\sqrt{21}}{14}$
14.如图,菱形ABCD的边长为10 cm,DE⊥AB,sinA = $\frac{3}{5}$,求DE的长和菱形ABCD的面积.


答案:
$\because DE\perp AB$,$\therefore \angle AED = 90^{\circ}$,在$Rt\triangle AED$中,$\sin A=\frac{DE}{AD}$,即$\frac{3}{5}=\frac{DE}{10}$,解得$DE = 6\ cm$,$\therefore$菱形$ABCD$的面积为$10\times6 = 60(cm^{2})$
15.如图,网格中的每个小正方形的边长都是1,△ABC的每个顶点都在网格的交点处,求sinA的值.


答案:
作$AD\perp BC$于点$D$,$CE\perp AB$于点$E$,由勾股定理得$AB = AC = 2\sqrt{5}$,$BC = 2\sqrt{2}$,$\therefore \triangle ABC$为等腰三角形,$\therefore D$为$BC$的中点,即点$D$在格点上,由勾股定理得$AD = 3\sqrt{2}$,由$\triangle ABC$的面积可得$BC\cdot AD = AB\cdot CE$,$\therefore CE=\frac{2\sqrt{2}\times3\sqrt{2}}{2\sqrt{5}}=\frac{6\sqrt{5}}{5}$,$\therefore \sin A=\frac{CE}{AC}=\frac{\frac{6\sqrt{5}}{5}}{2\sqrt{5}}=\frac{3}{5}$
16.如图,AB是半圆的直径,点O为圆心,OA = 5,弦AC = 8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC = α,求sinα的值.


答案:
连接$BC$,$\because AB$是半圆的直径,$\therefore \angle ACB = 90^{\circ}$,在$Rt\triangle ABC$中,$AC = 8$,$AB = 10$,$\therefore BC = \sqrt{AB^{2}-AC^{2}} = 6$,$\because OD\perp AC$,$\therefore AE = CE=\frac{1}{2}AC = 4$,在$Rt\triangle BCE$中,$BE = \sqrt{BC^{2}+CE^{2}} = 2\sqrt{13}$,$\therefore \sin\alpha=\frac{BC}{BE}=\frac{6}{2\sqrt{13}}=\frac{3\sqrt{13}}{13}$
查看更多完整答案,请扫码查看


