1.(南阳西峡县期末)如图,已知$AB$是$\odot O$的直径,$\odot O$的半径为$1$,$BD = \sqrt{3}$,则$\sin\angle C$的值等于 ( )
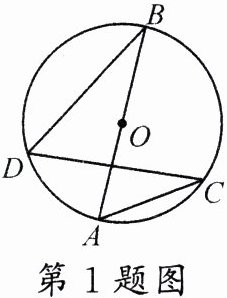
A.$\frac{1}{2}$
B.$\frac{\sqrt{3}}{2}$
C.$\frac{\sqrt{3}}{3}$
D.$\frac{\sqrt{2}}{2}$

A.$\frac{1}{2}$
B.$\frac{\sqrt{3}}{2}$
C.$\frac{\sqrt{3}}{3}$
D.$\frac{\sqrt{2}}{2}$
答案:
A
2.(河南模拟)如图,$\odot O$的直径$BD = 4$,$\angle A = 60^{\circ}$,则$BC$的长度为 ( )
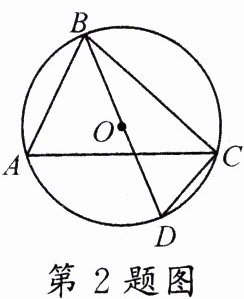
A.$\sqrt{3}$
B.$2$
C.$2\sqrt{3}$
D.$4\sqrt{3}$

A.$\sqrt{3}$
B.$2$
C.$2\sqrt{3}$
D.$4\sqrt{3}$
答案:
C
3.(2024·郑州期中)如图,点$A$,$B$,$C$分别在$\odot O$上,连接$OA$,$OB$,$AC$,$BC$,若$\cos\angle AOB = \frac{5}{13}$,则$\tan C$的值为 ( )

A.$\frac{1}{5}$
B.$\frac{1}{3}$
C.$\frac{2}{3}$
D.$\frac{6}{5}$

A.$\frac{1}{5}$
B.$\frac{1}{3}$
C.$\frac{2}{3}$
D.$\frac{6}{5}$
答案:
C
4.(凉山州中考)如图,$\odot O$的直径$AB$经过弦$CD$的中点$H$,若$\cos\angle CDB = \frac{4}{5}$,$BD = 5$,则$\odot O$的半径为_______.
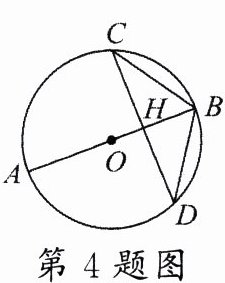

答案:
$\frac{25}{6}$
5.如图,$\odot O$是$\triangle ABC$的外接圆,$AD$是$\odot O$的直径,若$\odot O$的半径是$4$,$\sin B = \frac{1}{4}$,则线段$AC$的长为____.
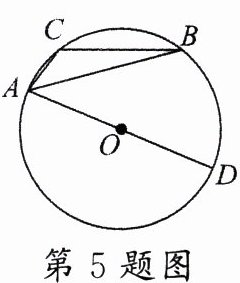

答案:
2
6.如图,直线$MN$与$\odot O$相切于点$M$,$ME = EF$且$EF// MN$,则$\cos E =$_______.
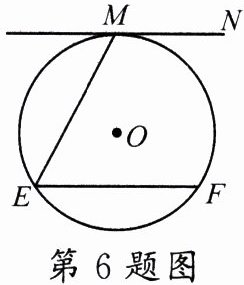

答案:
$\frac{1}{2}$
7.(牡丹江中考)$AB$是$\odot O$的弦,$OM\perp AB$,垂足为$M$,连接$OA$.若$\triangle AOM$中有一个角是$30^{\circ}$,$OM = 2\sqrt{3}$,则弦$AB$的长为________.
答案:
12或4
8.(2024·济南)如图,$AB$,$CD$为$\odot O$的直径,点$E$在$\overset{\frown}{BD}$上,连接$AE$,$DE$,点$G$在$BD$的延长线上,$AB = AG$,$\angle EAD+\angle EDB = 45^{\circ}$.
(1)求证:$AG$与$\odot O$相切;
(2)若$BG = 4\sqrt{5}$,$\sin\angle DAE = \frac{1}{3}$,求$DE$的长.
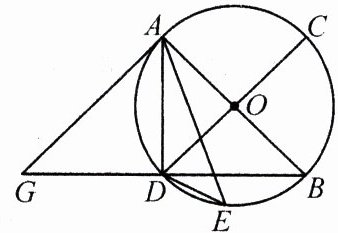
(1)求证:$AG$与$\odot O$相切;
(2)若$BG = 4\sqrt{5}$,$\sin\angle DAE = \frac{1}{3}$,求$DE$的长.

答案:
(1) 因为∠EDB,∠EAB所对的弧是同弧,所以∠EDB = ∠EAB,因为∠EAD + ∠EDB = 45°,所以∠EAD + ∠EAB = 45°,即∠BAD = 45°,因为AB为直径,所以∠ADB = 90°,所以∠B = 45°,因为AB = AG,所以∠B = ∠G = 45°,所以∠GAB = 90°,因为AB为⊙O的直径,所以AG与⊙O相切。
(2) 连接CE,因为∠DAE,∠DCE所对的弧是同弧,所以∠DAE = ∠DCE,因为DC为直径,所以∠DEC = 90°,在Rt△DEC中,sin∠DCE = sin∠DAE = $\frac{1}{3}$ = $\frac{DE}{DC}$,因为BG = 4$\sqrt{5}$,∠B = 45°,∠BAG = 90°,所以AB = $\frac{\sqrt{2}}{2}$BG = 2$\sqrt{10}$ = DC,所以DE = DCsin∠DAE = 2$\sqrt{10}$×$\frac{1}{3}$ = $\frac{2\sqrt{10}}{3}$。
(1) 因为∠EDB,∠EAB所对的弧是同弧,所以∠EDB = ∠EAB,因为∠EAD + ∠EDB = 45°,所以∠EAD + ∠EAB = 45°,即∠BAD = 45°,因为AB为直径,所以∠ADB = 90°,所以∠B = 45°,因为AB = AG,所以∠B = ∠G = 45°,所以∠GAB = 90°,因为AB为⊙O的直径,所以AG与⊙O相切。
(2) 连接CE,因为∠DAE,∠DCE所对的弧是同弧,所以∠DAE = ∠DCE,因为DC为直径,所以∠DEC = 90°,在Rt△DEC中,sin∠DCE = sin∠DAE = $\frac{1}{3}$ = $\frac{DE}{DC}$,因为BG = 4$\sqrt{5}$,∠B = 45°,∠BAG = 90°,所以AB = $\frac{\sqrt{2}}{2}$BG = 2$\sqrt{10}$ = DC,所以DE = DCsin∠DAE = 2$\sqrt{10}$×$\frac{1}{3}$ = $\frac{2\sqrt{10}}{3}$。
9.(通辽中考)如图,在$Rt\triangle AOB$中,$\angle AOB = 90^{\circ}$,以$O$为圆心,$OB$的长为半径的圆交边$AB$于点$D$,点$C$在边$OA$上且$CD = AC$,延长$CD$交$OB$的延长线于点$E$.
(1)求证:$CD$是$\odot O$的切线;
(2)已知$\sin\angle OCD = \frac{4}{5}$,$AB = 4\sqrt{5}$,求$AC$的长度及阴影部分面积.
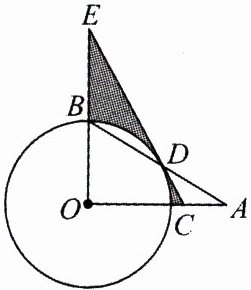
(1)求证:$CD$是$\odot O$的切线;
(2)已知$\sin\angle OCD = \frac{4}{5}$,$AB = 4\sqrt{5}$,求$AC$的长度及阴影部分面积.

答案:
(1) 连接OD,因为AC = CD,所以∠A = ∠ADC = ∠BDE,因为∠AOB = 90°,所以∠A + ∠ABO = 90°,又因为OB = OD,所以∠OBD = ∠ODB,所以∠ODB + ∠BDE = 90°,即OD⊥EC,因为OD是半径,所以CD是⊙O的切线。
(2) 在Rt△COD中,设OD = 4x,则OC = 5x,所以CD = $\sqrt{OC^{2}-OD^{2}}$ = 3x = AC,在Rt△AOB中,OB = OD = 4x,OA = OC + AC = 8x,AB = 4$\sqrt{5}$,由勾股定理,得OB² + OA² = AB²,即(4x)² + (8x)² = (4$\sqrt{5}$)²,解得x = 1或x = -1(舍去),所以AC = CD = 3x = 3,OC = 5x = 5,OB = OD = 4x = 4,因为∠ODC = ∠EOC = 90°,∠OCD = ∠ECO,所以△COD∽△CEO,所以$\frac{OC}{EC}$ = $\frac{CD}{OC}$,即$\frac{5}{EC}$ = $\frac{3}{5}$,所以EC = $\frac{25}{3}$,设⊙O与OA交于点F,则S阴影 = S△COE - S扇形BOF = $\frac{1}{2}$×$\frac{25}{3}$×4 - $\frac{90\pi×4^{2}}{360}$ = $\frac{50}{3}$ - 4π。
(1) 连接OD,因为AC = CD,所以∠A = ∠ADC = ∠BDE,因为∠AOB = 90°,所以∠A + ∠ABO = 90°,又因为OB = OD,所以∠OBD = ∠ODB,所以∠ODB + ∠BDE = 90°,即OD⊥EC,因为OD是半径,所以CD是⊙O的切线。
(2) 在Rt△COD中,设OD = 4x,则OC = 5x,所以CD = $\sqrt{OC^{2}-OD^{2}}$ = 3x = AC,在Rt△AOB中,OB = OD = 4x,OA = OC + AC = 8x,AB = 4$\sqrt{5}$,由勾股定理,得OB² + OA² = AB²,即(4x)² + (8x)² = (4$\sqrt{5}$)²,解得x = 1或x = -1(舍去),所以AC = CD = 3x = 3,OC = 5x = 5,OB = OD = 4x = 4,因为∠ODC = ∠EOC = 90°,∠OCD = ∠ECO,所以△COD∽△CEO,所以$\frac{OC}{EC}$ = $\frac{CD}{OC}$,即$\frac{5}{EC}$ = $\frac{3}{5}$,所以EC = $\frac{25}{3}$,设⊙O与OA交于点F,则S阴影 = S△COE - S扇形BOF = $\frac{1}{2}$×$\frac{25}{3}$×4 - $\frac{90\pi×4^{2}}{360}$ = $\frac{50}{3}$ - 4π。
查看更多完整答案,请扫码查看


