10.(2024·泸州)已知关于$x$的一元二次方程$x^2 + 2x + 1 - k = 0$无实数根,则函数$y = kx$与函数$y = \frac{2}{x}$的图象交点个数为 ( )
A.0
B.1
C.2
D.3
A.0
B.1
C.2
D.3
答案:
A
11.(2024·齐齐哈尔)如图,反比例函数$y = \frac{k}{x}(x < 0)$的图象经过平行四边形$ABCO$的顶点$A$,$OC$在$x$轴上,若点$B(-1,3)$,$S_{\square ABCO} = 3$,则实数$k$的值为_______.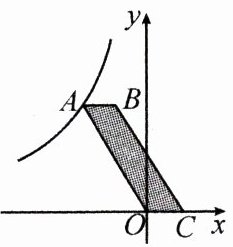

答案:
-6
12.(河南中考改编)如图,大、小两个正方形的中心均与平面直角坐标系的原点$O$重合,边分别与坐标轴平行,反比例函数$y = \frac{k}{x}$的图象与大正方形的一边交于点$A(1,2)$,且经过小正方形的顶点$B$.则图中阴影部分的面积为_____.
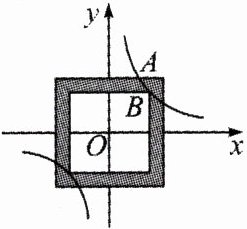

答案:
8
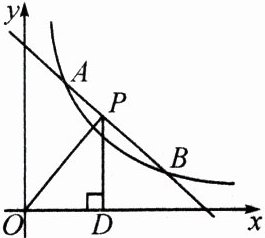
13.(河南中考)如图,一次函数$y = -x + b$与反比例函数$y = \frac{k}{x}(x > 0)$的图象交于点$A(m,3)$和$B(3,1)$.
(1)填空:
①一次函数的解析式为____________;
②反比例函数的解析式为____________;
(2)点$P$是线段$AB$上一点,过点$P$作$PD \perp x$轴于点$D$,连接$OP$.若$\triangle POD$的面积为$S$,求$S$的取值范围.
(1)填空:
①一次函数的解析式为____________;
②反比例函数的解析式为____________;
(2)点$P$是线段$AB$上一点,过点$P$作$PD \perp x$轴于点$D$,连接$OP$.若$\triangle POD$的面积为$S$,求$S$的取值范围.

答案:
$y = -x + 4$@@$y = \frac{3}{x}$@@
(2)
∵点$A(m,3)$在$y = \frac{3}{x}$的图象上,
∴$\frac{3}{m}=3$,
∴$m = 1$,
∴$A(1,3)$。而点$P$在线段$AB$上,设点$P(n,-n + 4)$,则$1\leqslant n\leqslant3$,
∴$S = \frac{1}{2}OD\cdot PD=\frac{1}{2}\times n(-n + 4)=-\frac{1}{2}(n - 2)^2 + 2$。
∵$-\frac{1}{2}\lt0$,且$1\leqslant n\leqslant3$,
∴当$n = 2$时,$S_{最大}=2$;当$n = 1$或3时,$S_{最小}=\frac{3}{2}$,
∴$S$的取值范围是$\frac{3}{2}\leqslant S\leqslant2$
(2)
∵点$A(m,3)$在$y = \frac{3}{x}$的图象上,
∴$\frac{3}{m}=3$,
∴$m = 1$,
∴$A(1,3)$。而点$P$在线段$AB$上,设点$P(n,-n + 4)$,则$1\leqslant n\leqslant3$,
∴$S = \frac{1}{2}OD\cdot PD=\frac{1}{2}\times n(-n + 4)=-\frac{1}{2}(n - 2)^2 + 2$。
∵$-\frac{1}{2}\lt0$,且$1\leqslant n\leqslant3$,
∴当$n = 2$时,$S_{最大}=2$;当$n = 1$或3时,$S_{最小}=\frac{3}{2}$,
∴$S$的取值范围是$\frac{3}{2}\leqslant S\leqslant2$
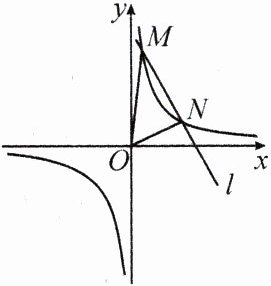
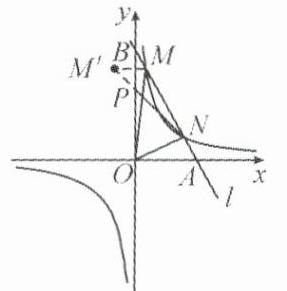
14.(2024·雅安)如图,在平面直角坐标系中,一次函数的图象$l$与反比例函数$y = \frac{k}{x}$的图象交于$M(\frac{1}{2},4),N(n,1)$两点.
(1)求反比例函数及一次函数的解析式;
(2)求$\triangle OMN$的面积;
(3)若点$P$是$y$轴上一动点,连接$PM,PN$.当$PM + PN$的值最小时,求点$P$的坐标.
(1)求反比例函数及一次函数的解析式;
(2)求$\triangle OMN$的面积;
(3)若点$P$是$y$轴上一动点,连接$PM,PN$.当$PM + PN$的值最小时,求点$P$的坐标.

答案:
(1)
∵$M(\frac{1}{2},4)$在反比例函数$y = \frac{k}{x}$的图象上,
∴$k = \frac{1}{2}\times4 = 2$,
∴反比例函数解析式为$y = \frac{2}{x}$。又
∵$N(n,1)$在反比例函数$y = \frac{2}{x}$上,
∴$n = 2$,
∴$N(2,1)$。设一次函数解析式为$y = ax + b$,
∴$\begin{cases}\frac{1}{2}a + b = 4\\2a + b = 1\end{cases}$,
∴$\begin{cases}a = -2\\b = 5\end{cases}$,
∴一次函数的解析式为$y = -2x + 5$
(2)如图,设直线$l$交$x$轴于点$A$,交$y$轴于点$B$,
∵直线$l$为$y = -2x + 5$,
∴$A(\frac{5}{2},0)$,$B(0,5)$,
∴$OA = \frac{5}{2}$,$OB = 5$,
∴$S_{\triangle{OMN}} = S_{\triangle{AOB}} - S_{\triangle{AON}} - S_{\triangle{BOM}}=\frac{1}{2}AO\cdot BO - \frac{1}{2}AO\cdot y_N - \frac{1}{2}BO\times x_M=\frac{1}{2}\times\frac{5}{2}\times5 - \frac{1}{2}\times\frac{5}{2}\times1 - \frac{1}{2}\times5\times\frac{1}{2}=\frac{15}{4}$
(3)如图,作点$M$关于$y$轴的对称点$M'$,连接$M'N$交$y$轴于点$P$,则$PM + PN$的最小值等于$M'N$的长。
∵$M(\frac{1}{2},4)$与$M'$关于$y$轴对称,
∴$M'(-\frac{1}{2},4)$。又$N(2,1)$,
∴直线$M'N$为$y = -\frac{6}{5}x + \frac{17}{5}$。令$x = 0$,则$y = \frac{17}{5}$,
∴$P(0,\frac{17}{5})$
(1)
∵$M(\frac{1}{2},4)$在反比例函数$y = \frac{k}{x}$的图象上,
∴$k = \frac{1}{2}\times4 = 2$,
∴反比例函数解析式为$y = \frac{2}{x}$。又
∵$N(n,1)$在反比例函数$y = \frac{2}{x}$上,
∴$n = 2$,
∴$N(2,1)$。设一次函数解析式为$y = ax + b$,
∴$\begin{cases}\frac{1}{2}a + b = 4\\2a + b = 1\end{cases}$,
∴$\begin{cases}a = -2\\b = 5\end{cases}$,
∴一次函数的解析式为$y = -2x + 5$
(2)如图,设直线$l$交$x$轴于点$A$,交$y$轴于点$B$,
∵直线$l$为$y = -2x + 5$,
∴$A(\frac{5}{2},0)$,$B(0,5)$,
∴$OA = \frac{5}{2}$,$OB = 5$,
∴$S_{\triangle{OMN}} = S_{\triangle{AOB}} - S_{\triangle{AON}} - S_{\triangle{BOM}}=\frac{1}{2}AO\cdot BO - \frac{1}{2}AO\cdot y_N - \frac{1}{2}BO\times x_M=\frac{1}{2}\times\frac{5}{2}\times5 - \frac{1}{2}\times\frac{5}{2}\times1 - \frac{1}{2}\times5\times\frac{1}{2}=\frac{15}{4}$
(3)如图,作点$M$关于$y$轴的对称点$M'$,连接$M'N$交$y$轴于点$P$,则$PM + PN$的最小值等于$M'N$的长。
∵$M(\frac{1}{2},4)$与$M'$关于$y$轴对称,
∴$M'(-\frac{1}{2},4)$。又$N(2,1)$,
∴直线$M'N$为$y = -\frac{6}{5}x + \frac{17}{5}$。令$x = 0$,则$y = \frac{17}{5}$,
∴$P(0,\frac{17}{5})$

查看更多完整答案,请扫码查看


