3.(2024·河南)在学习特殊四边形的过程中,我们积累了一定的研究经验.请运用已有经验,对“邻等对补四边形”进行研究.
定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.
(1)操作判断
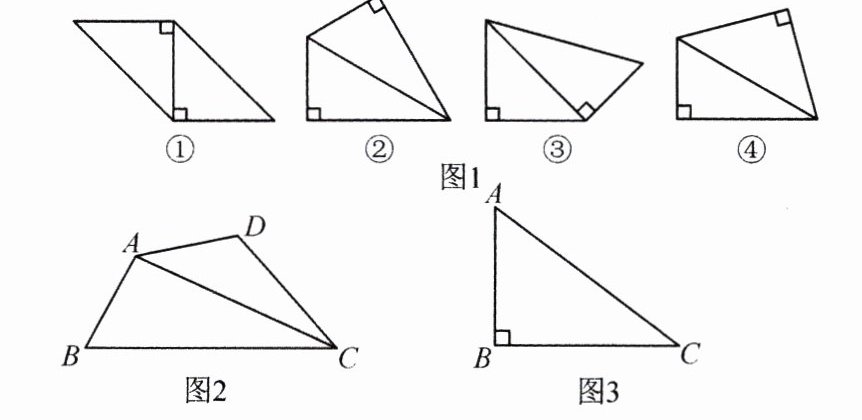
用分别含有30°和45°角的直角三角形纸板拼出如图1所示的4个四边形,其中是邻等对补四边形的有 (填序号);
(2)性质探究
根据定义可得出邻等对补四边形的边、角的性质.下面研究与对角线相关的性质.
如图2,四边形ABCD是邻等对补四边形,AB = AD,AC是它的一条对角线.
①写出图中相等的角,并说明理由;
②若BC = m,DC = n,∠BCD = 2θ,求AC的长(用含m,n,θ的式子表示);
(3)拓展应用
如图3,在Rt△ABC中,∠B = 90°,AB = 3,BC = 4,分别在边BC,AC上取点M,N,使四边形ABMN是邻等对补四边形.当该邻等对补四边形仅有一组邻边相等时,请直接写出BN的长.
定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.
(1)操作判断
用分别含有30°和45°角的直角三角形纸板拼出如图1所示的4个四边形,其中是邻等对补四边形的有 (填序号);
(2)性质探究
根据定义可得出邻等对补四边形的边、角的性质.下面研究与对角线相关的性质.
如图2,四边形ABCD是邻等对补四边形,AB = AD,AC是它的一条对角线.
①写出图中相等的角,并说明理由;
②若BC = m,DC = n,∠BCD = 2θ,求AC的长(用含m,n,θ的式子表示);
(3)拓展应用
如图3,在Rt△ABC中,∠B = 90°,AB = 3,BC = 4,分别在边BC,AC上取点M,N,使四边形ABMN是邻等对补四边形.当该邻等对补四边形仅有一组邻边相等时,请直接写出BN的长.

答案:
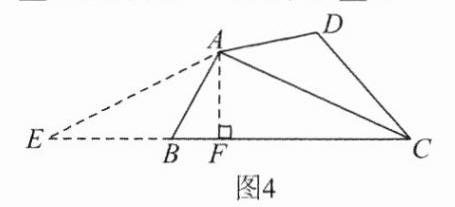
②④@@$\angle ACD = \angle ACB$, 理由: 如图 4, 延长 $CB$ 至点 $E$, 使 $BE = DC$, 连接 $AE$, $\because$ 四边形 $ABCD$ 是邻等对补四边形, $\therefore \angle ABC + \angle D = 180^{\circ}$, $\because \angle ABC + \angle ABE = 180^{\circ}$, $\therefore \angle ABE = \angle D$, $\because AB = AD$, $\therefore \triangle ABE \cong \triangle ADC(SAS)$, $\therefore \angle E = \angle ACD$, $AE = AC$, $\therefore \angle E = \angle ACB$, $\therefore \angle ACD = \angle ACB$@@如图 4, 过 $A$ 作 $AF \perp EC$ 于 $F$, $\because AE = AC$, $\therefore CF = \frac{1}{2}CE = \frac{1}{2}(BC + BE) = \frac{1}{2}(BC + DC) = \frac{m + n}{2}$, $\because \angle BCD = 2\theta$, $\therefore \angle ACD = \angle ACB = \theta$, 在 $Rt\triangle AFC$ 中, $\cos\theta = \frac{CF}{AC}$, $\therefore AC = \frac{CF}{\cos\theta} = \frac{m + n}{2\cos\theta}$@@$\because \angle B = 90^{\circ}$, $AB = 3$, $BC = 4$, $\therefore AC = \sqrt{AB^{2} + BC^{2}} = 5$, $\because$ 四边形 $ABMN$ 是邻等对补四边形, $\therefore \angle ANM + \angle B = 180^{\circ}$, $\therefore \angle ANM = 90^{\circ}$, 当 $AB = BM$ 时, 如图 5, 连接 $AM$, 过 $N$ 作 $NH \perp BC$ 于 $H$, $\therefore AM^{2} = AB^{2} + BM^{2} = 18$, 在 $Rt\triangle AMN$ 中, $MN^{2} = AM^{2} - AN^{2} = 18 - AN^{2}$, 在 $Rt\triangle CMN$ 中, $MN^{2} = CM^{2} - CN^{2} = (4 - 3)^{2} - (5 - AN)^{2}$, $18 - AN^{2} = (4 - 3)^{2} - (5 - AN)^{2}$, 解得 $AN = 4.2$, $\therefore CN = 0.8$, $\because \angle NHC = \angle ABC = 90^{\circ}$, $\angle C = \angle C$, $\therefore \triangle NHC \sim \triangle ABC$, $\therefore \frac{NC}{AC} = \frac{NH}{AB} = \frac{CH}{CB}$, 即 $\frac{0.8}{5} = \frac{NH}{3} = \frac{CH}{4}$, $\therefore NH = \frac{12}{25}$, $CH = \frac{16}{25}$, $\therefore BH = \frac{84}{25}$, $\therefore BN = \sqrt{BH^{2} + NH^{2}} = \frac{12}{5}\sqrt{2}$; 当 $AN = AB$ 时, 如图 6, 连接 $AM$, $\because AM = AM$, $\therefore Rt\triangle ABM \cong Rt\triangle ANM(HL)$, $\therefore BM = NM$, 不符合题意, 舍去; 当 $AN = MN$ 时, 如图 7, 连接 $AM$, 过 $N$ 作 $NH \perp BC$ 于 $H$, $\because \angle MNC = \angle ABC = 90^{\circ}$, $\angle C = \angle C$, $\therefore \triangle CMN \sim \triangle CAB$, 即 $\frac{CN}{CB} = \frac{MN}{AB} = \frac{AN}{AB}$, 即 $\frac{CN}{4} = \frac{5 - CN}{3}$, 解得 $CN = \frac{20}{7}$, $\because \angle NHC = \angle ABC = 90^{\circ}$, $\angle C = \angle C$, $\therefore \triangle NHC \sim \triangle ABC$, $\therefore \frac{NC}{AC} = \frac{NH}{AB} = \frac{CH}{CB}$, 即 $\frac{\frac{20}{7}}{5} = \frac{NH}{3} = \frac{CH}{4}$, $\therefore NH = \frac{12}{7}$, $CH = \frac{16}{7}$, $\therefore BH = \frac{12}{7}$, $\therefore BN = \sqrt{BH^{2} + NH^{2}} = \frac{12}{7}\sqrt{2}$, 当 $BM = MN$ 时, 如图 8, 连接 $AM$, $\because AM = AM$, $\therefore Rt\triangle ABM \cong Rt\triangle ANM(HL)$, $\therefore AN = AB$, 不符合题意, 舍去. 综上, $BN$ 的长为 $\frac{12}{5}\sqrt{2}$ 或 $\frac{12}{7}\sqrt{2}$

②④@@$\angle ACD = \angle ACB$, 理由: 如图 4, 延长 $CB$ 至点 $E$, 使 $BE = DC$, 连接 $AE$, $\because$ 四边形 $ABCD$ 是邻等对补四边形, $\therefore \angle ABC + \angle D = 180^{\circ}$, $\because \angle ABC + \angle ABE = 180^{\circ}$, $\therefore \angle ABE = \angle D$, $\because AB = AD$, $\therefore \triangle ABE \cong \triangle ADC(SAS)$, $\therefore \angle E = \angle ACD$, $AE = AC$, $\therefore \angle E = \angle ACB$, $\therefore \angle ACD = \angle ACB$@@如图 4, 过 $A$ 作 $AF \perp EC$ 于 $F$, $\because AE = AC$, $\therefore CF = \frac{1}{2}CE = \frac{1}{2}(BC + BE) = \frac{1}{2}(BC + DC) = \frac{m + n}{2}$, $\because \angle BCD = 2\theta$, $\therefore \angle ACD = \angle ACB = \theta$, 在 $Rt\triangle AFC$ 中, $\cos\theta = \frac{CF}{AC}$, $\therefore AC = \frac{CF}{\cos\theta} = \frac{m + n}{2\cos\theta}$@@$\because \angle B = 90^{\circ}$, $AB = 3$, $BC = 4$, $\therefore AC = \sqrt{AB^{2} + BC^{2}} = 5$, $\because$ 四边形 $ABMN$ 是邻等对补四边形, $\therefore \angle ANM + \angle B = 180^{\circ}$, $\therefore \angle ANM = 90^{\circ}$, 当 $AB = BM$ 时, 如图 5, 连接 $AM$, 过 $N$ 作 $NH \perp BC$ 于 $H$, $\therefore AM^{2} = AB^{2} + BM^{2} = 18$, 在 $Rt\triangle AMN$ 中, $MN^{2} = AM^{2} - AN^{2} = 18 - AN^{2}$, 在 $Rt\triangle CMN$ 中, $MN^{2} = CM^{2} - CN^{2} = (4 - 3)^{2} - (5 - AN)^{2}$, $18 - AN^{2} = (4 - 3)^{2} - (5 - AN)^{2}$, 解得 $AN = 4.2$, $\therefore CN = 0.8$, $\because \angle NHC = \angle ABC = 90^{\circ}$, $\angle C = \angle C$, $\therefore \triangle NHC \sim \triangle ABC$, $\therefore \frac{NC}{AC} = \frac{NH}{AB} = \frac{CH}{CB}$, 即 $\frac{0.8}{5} = \frac{NH}{3} = \frac{CH}{4}$, $\therefore NH = \frac{12}{25}$, $CH = \frac{16}{25}$, $\therefore BH = \frac{84}{25}$, $\therefore BN = \sqrt{BH^{2} + NH^{2}} = \frac{12}{5}\sqrt{2}$; 当 $AN = AB$ 时, 如图 6, 连接 $AM$, $\because AM = AM$, $\therefore Rt\triangle ABM \cong Rt\triangle ANM(HL)$, $\therefore BM = NM$, 不符合题意, 舍去; 当 $AN = MN$ 时, 如图 7, 连接 $AM$, 过 $N$ 作 $NH \perp BC$ 于 $H$, $\because \angle MNC = \angle ABC = 90^{\circ}$, $\angle C = \angle C$, $\therefore \triangle CMN \sim \triangle CAB$, 即 $\frac{CN}{CB} = \frac{MN}{AB} = \frac{AN}{AB}$, 即 $\frac{CN}{4} = \frac{5 - CN}{3}$, 解得 $CN = \frac{20}{7}$, $\because \angle NHC = \angle ABC = 90^{\circ}$, $\angle C = \angle C$, $\therefore \triangle NHC \sim \triangle ABC$, $\therefore \frac{NC}{AC} = \frac{NH}{AB} = \frac{CH}{CB}$, 即 $\frac{\frac{20}{7}}{5} = \frac{NH}{3} = \frac{CH}{4}$, $\therefore NH = \frac{12}{7}$, $CH = \frac{16}{7}$, $\therefore BH = \frac{12}{7}$, $\therefore BN = \sqrt{BH^{2} + NH^{2}} = \frac{12}{7}\sqrt{2}$, 当 $BM = MN$ 时, 如图 8, 连接 $AM$, $\because AM = AM$, $\therefore Rt\triangle ABM \cong Rt\triangle ANM(HL)$, $\therefore AN = AB$, 不符合题意, 舍去. 综上, $BN$ 的长为 $\frac{12}{5}\sqrt{2}$ 或 $\frac{12}{7}\sqrt{2}$


查看更多完整答案,请扫码查看


