《2025年原创新课堂九年级数学下册人教版》

1. 有甲、乙两个三角形木框，甲三角形木框的三边长分别为1，$\sqrt{2}$，$\sqrt{5}$，乙三角形木框的三边长分别为5，$\sqrt{5}$，$\sqrt{10}$，则甲、乙两个三角形（ ）
A. 一定相似
B. 一定不相似
C. 不一定相似
D. 无法判断

答案： A

2. 已知$\triangle ABC$的三边长分别为6 cm，7.5 cm，9 cm，$\triangle DEF$的一边长为4 cm，当$\triangle DEF$的另两边长是下列哪一组数据时，这两个三角形相似（ ）
A. 2 cm，3 cm
B. 4 cm，5 cm
C. 5 cm，6 cm
D. 6 cm，7 cm

答案： C

3.（教材P34练习1变式）依据下列各组条件，说明$\triangle ABC$和$\triangle A'B'C'$是否相似：
（1）$AB = 12$，$BC = 15$，$AC = 24$，$A'B' = 25$，$B'C' = 40$，$A'C' = 20$；
（2）$AB = 3$，$BC = 4$，$AC = 5$，$A'B' = 12$，$B'C' = 16$，$A'C' = 22$；
（3）$\triangle A'B'C'$是$\triangle ABC$的三条中位线组成的三角形.

答案： \n（1）由题意知$\frac{AB}{A'C'}=\frac{BC}{A'B'}=\frac{AC}{B'C'}=\frac{3}{5}$，$\therefore\triangle ABC\sim\triangle C'A'B'$\n（2）由题意知$\frac{AB}{A'B'}=\frac{1}{4}$，$\frac{BC}{B'C'}=\frac{1}{4}$，$\frac{AC}{A'C'}=\frac{5}{22}$，$\therefore\frac{AB}{A'B'}=\frac{BC}{B'C'}\neq\frac{AC}{A'C'}$，$\therefore\triangle ABC$与$\triangle A'B'C'$不相似\n（3）$\because\triangle A'B'C'$是$\triangle ABC$的三条中位线组成的三角形，$\therefore\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}=2$，$\therefore\triangle ABC\sim\triangle A'B'C'}$

4. 如图，已知$\triangle ABC$，则下列四个三角形中，与$\triangle ABC$相似的是（ ）

答案： C

5. 如图，四边形$ABCD$的对角线$AC$，$BD$相交于点$O$，且将这个四边形分成①，②，③，④四个三角形. 若$OA:OC = OB:OD$，则下列结论中一定正确的是（ ）

A. ①和②相似
B. ①和③相似
C. ①和④相似
D. ②和④相似

答案： B

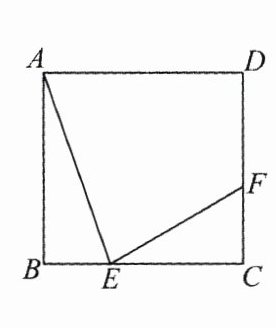
6.（2024·广州）如图，点$E$，$F$分别在正方形$ABCD$的边$BC$，$CD$上，$BE = 3$，$EC = 6$，$CF = 2$. 求证：$\triangle ABE\backsim\triangle ECF$.

答案： 证明：$\because BE = 3$，$EC = 6$，$CF = 2$，$\therefore BC=3 + 6 = 9$，$\because$四边形$ABCD$是正方形，$\therefore AB = BC = 9$，$\angle B=\angle C = 90^{\circ}$，$\because\frac{AB}{CE}=\frac{9}{6}=\frac{3}{2}$，$\frac{BE}{CF}=\frac{3}{2}$，$\therefore\frac{AB}{CE}=\frac{BE}{CF}$，$\therefore\triangle ABE\sim\triangle ECF$