《2025年原创新课堂九年级数学下册人教版》

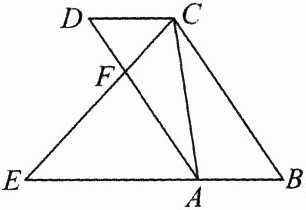
5.如图，四边形ABCD是平行四边形，点E在边BA的延长线上，CE交AD于点F，∠ECA = ∠D.求证：AC·BE = CE·AD.

 

答案： 因为四边形ABCD是平行四边形，所以BC = AD，CD//AB，AD//BC，所以∠D = ∠DAE = ∠B，因为∠ECA = ∠D，所以∠ECA = ∠B，因为∠E = ∠E，所以△EAC∽△ECB，所以AC : BC = CE : BE，所以AC·BE = CE·BC，所以AC·BE = CE·AD。

7.如图，在△ABC中，BD，CE是高，EH⊥BC于点H，交BD于点G，交CA的延长线于点M.求证：HE² = HG·MH.

 

答案： 因为CE⊥AB，EH⊥BC，所以∠EHB = ∠EHC = 90°，∠BEC = 90°，所以∠EBH + ∠BEH = 90°，∠BEH + ∠CEH = 90°，所以∠EBH = ∠CEH，因为∠EHB = ∠EHC，所以△BHE∽△EHC，所以$\frac{EH}{CH}=\frac{BH}{EH}$，所以EH² = CH·BH，因为BD⊥AC，所以∠DBC + ∠BCD = 90°，又因为∠M + ∠HCM = 90°，所以∠DBC = ∠M，因为∠GHB = ∠MHC = 90°，所以△BHG∽△MHC，所以$\frac{HG}{CH}=\frac{BH}{MH}$，所以HG·MH = CH·BH，所以HE² = HG·MH。

6.如图，过□ABCD的对角线AC上任一点P作一直线，分别交AB，BC，CD，DA所在直线于点E，F，G，H.求证：PE·PF = PG·PH.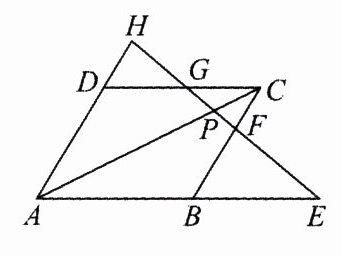

答案： 因为四边形ABCD为平行四边形，所以CD//AB，AD//BC，因为CG//AE，所以△PCG∽△PAE，所以$\frac{PC}{PA}=\frac{PG}{PE}$，因为CF//AH，所以△PCF∽△PAH，所以$\frac{PC}{PA}=\frac{PF}{PH}$，所以$\frac{PG}{PE}=\frac{PF}{PH}$，所以PE·PF = PG·PH。

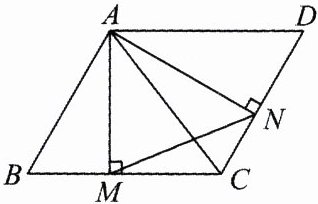
8.如图，在□ABCD中，AM⊥BC，AN⊥CD，垂足分别为M，N.
(1)求证：△AMB∽△AND；
(2)求证：$\frac{AM}{AB}=\frac{MN}{AC}$.

答案：
(1) 因为四边形ABCD为平行四边形，所以∠B = ∠D，AD = BC，因为AM⊥BC，AN⊥CD，所以∠AMB = ∠AND = 90°，所以△AMB∽△AND。
(2) 因为△AMB∽△AND，所以$\frac{AM}{AN}=\frac{AB}{AD}$，又因为AD = BC，所以$\frac{AM}{AN}=\frac{AB}{BC}$，即AM : AB = AN : BC①，因为AD//BC，所以∠DAM = ∠AMB = 90°，因为∠MAN = 90° - ∠DAN，∠D = 90° - ∠DAN，所以∠MAN = ∠D，又因为∠D = ∠B，所以∠B = ∠MAN②，由①②得△AMN∽△BAC，所以$\frac{AM}{AB}=\frac{MN}{AC}$。